Visión general
- ¿Qué es K significa Clustering?
- Implementación de K significa Clustering
- WCSS y método de codo para encontrar el número de conglomerados
- Implementación de Python de K significa Clustering
K means es uno de los algoritmos de aprendizaje automático no supervisados más populares utilizados para resolver problemas de clasificación. K Significa que segrega los datos sin etiquetar en varios grupos, llamados clústeres, en función de tener características similares, patrones comunes.
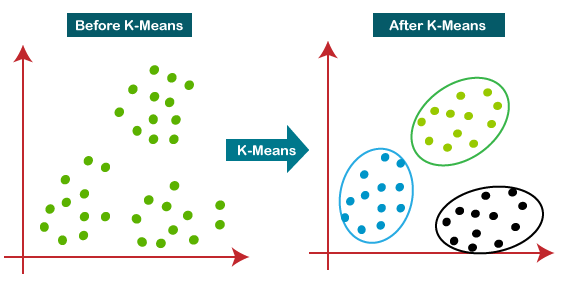
Tabla de contenido
- ¿Qué es la agrupación en clústeres?
- ¿Qué es el algoritmo de K significa?
- Implementación esquemática de la agrupación en clústeres de KMeans
- Elegir el número correcto de clústeres
- Implementación de Python
1. ¿Qué es la agrupación en clústeres?
Supongamos que tenemos un número N de conjuntos de datos multivariados sin etiquetar de varios animales como perros, gatos, pájaros, etc. La técnica para segregar conjuntos de datos en varios grupos, sobre la base de tener características y características similares, se denomina Clustering..
Los grupos que se forman se conocen como Clusters. La técnica de agrupación en clústeres se está utilizando en varios campos, como el reconocimiento de imágenes, el filtrado de correo no deseado
La agrupación en clústeres se utiliza en el algoritmo de aprendizaje no supervisadoEl aprendizaje no supervisado es una técnica de machine learning que permite a los modelos identificar patrones y estructuras en datos sin etiquetas predefinidas. A través de algoritmos como k-means y análisis de componentes principales, este enfoque se utiliza en diversas aplicaciones, como la segmentación de clientes, la detección de anomalías y la compresión de datos. Su capacidad para revelar información oculta lo convierte en una herramienta valiosa en la... en el aprendizaje automático como se pueden segregar datos multivariados en varios grupos, sin ningún supervisor, sobre la base de un patrón común oculto dentro de los conjuntos de datos.
2. ¿Qué es el algoritmo de K significa?
El algoritmo Kmeans es un algoritmo iterativo que divide un grupo de n conjuntos de datos en k subgrupos / clústeres en función de la similitud y su distancia media desde el centroide de ese subgrupo / formado en particular..
K, aquí está el número predefinido de clusters que formará el algoritmo. Si K = 3, significa que el número de conglomerados que se formarán a partir del conjunto de datos es 3
Pasos del algoritmo de K medias
El funcionamiento del algoritmo K-Means se explica en los siguientes pasos:
Paso 1: Seleccione el valor de K para decidir el número de conglomerados que se formarán.
Paso 2: Seleccione K puntos aleatorios que actuarán como centroides.
Paso 3: Asigne cada punto de datos, en función de su distancia desde los puntos seleccionados al azar (centroide), al centroide más cercano / cercano que formará los grupos predefinidos.
Paso 4: coloque un nuevo centroide de cada grupo.
Paso 5: Repita el paso 3, que reasigna cada punto de datos al nuevo centroide más cercano de cada grupo.
Paso 6: Si ocurre alguna reasignación, vaya al paso 4; de lo contrario, vaya al paso 7.
Paso 7: TERMINAR
3. Implementación esquemática de la agrupación en clústeres de K medias
PASO 1:Elijamos el número k de conglomerados, es decir, K = 2, para segregar el conjunto de datos y colocarlos en diferentes conglomerados respectivos. Elegiremos algunos 2 puntos aleatorios que actuarán como centroide para formar el grupo.
PASO 2: Ahora asignaremos cada punto de datos a un diagrama de dispersiónEl diagrama de dispersión es una herramienta gráfica utilizada en estadística para visualizar la relación entre dos variables. Consiste en un conjunto de puntos en un plano cartesiano, donde cada punto representa un par de valores correspondientes a las variables analizadas. Este tipo de gráfico permite identificar patrones, tendencias y posibles correlaciones, facilitando la interpretación de datos y la toma de decisiones basadas en la información visual presentada.... basado en su distancia desde el punto K o centroide más cercano. Se hará dibujando una medianaLa mediana es una medida estadística que representa el valor central de un conjunto de datos ordenados. Para calcularla, se organizan los datos de menor a mayor y se identifica el número que se encuentra en el medio. Si hay un número par de observaciones, se promedia los dos valores centrales. Este indicador es especialmente útil en distribuciones asimétricas, ya que no se ve afectado por valores extremos.... entre ambos centroides. Considere la siguiente imagen:
PASO 3: los puntos del lado izquierdo de la línea están cerca del centroide azul y los puntos a la derecha de la línea están cerca del centroide amarillo. El de la izquierda forma un grupo con centroide azul y el de la derecha con el centroide amarillo.
PASO 4:repita el proceso eligiendo un nuevo centroide. Para elegir los nuevos centroides, encontraremos el nuevo centro de gravedad de estos centroides, que se muestra a continuación:
PASO 5: A continuación, reasignaremos cada punto de datos al nuevo centroide. Repetiremos el mismo proceso anterior (usando una línea mediana). El punto de datos amarillo en el lado azul de la línea mediana se incluirá en el grupo azul
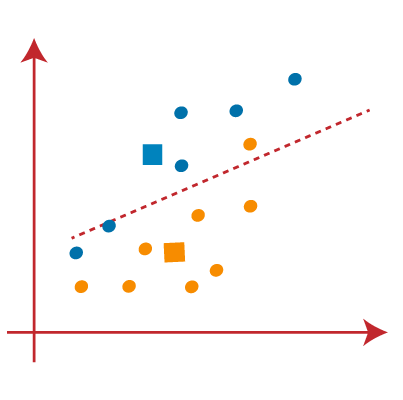
PASO 6: A medidaLa "medida" es un concepto fundamental en diversas disciplinas, que se refiere al proceso de cuantificar características o magnitudes de objetos, fenómenos o situaciones. En matemáticas, se utiliza para determinar longitudes, áreas y volúmenes, mientras que en ciencias sociales puede referirse a la evaluación de variables cualitativas y cuantitativas. La precisión en la medición es crucial para obtener resultados confiables y válidos en cualquier investigación o aplicación práctica.... que se haya realizado la reasignación, repetiremos el paso anterior de encontrar nuevos centroides.
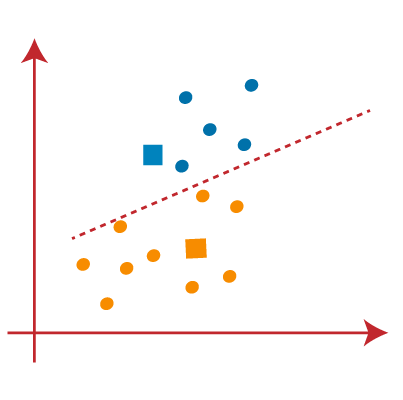
PASO 7: Repetiremos el proceso anterior de encontrar el centro de gravedad de los centroides, como se muestra a continuación.
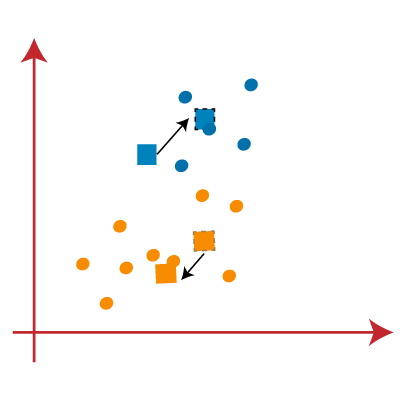
PASO 8: Después de encontrar los nuevos centroides, dibujaremos nuevamente la línea mediana y reasignaremos los puntos de datos, como en los pasos anteriores.
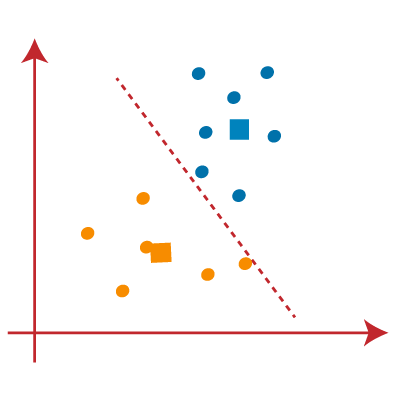
PASO 9: Finalmente, segregaremos puntos basados en la línea mediana, de manera que se formen dos grupos y ningún punto diferente se incluya en un solo grupo.
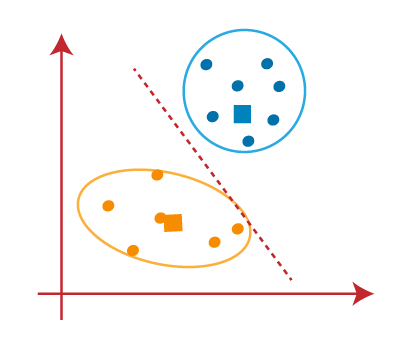
El grupo final que se está formando es el siguiente
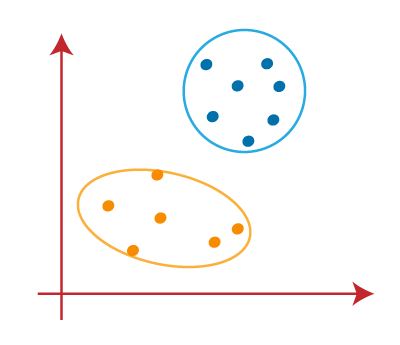
4. Elegir el número correcto de clústeres
El número de clústeres que elegimos para el algoritmo no debe ser aleatorio. Todos y cada uno de los conglomerados se forman calculando y comparando las distancias medias de cada punto de datos dentro de un conglomerado desde su centroide.
Podemos elegir el número correcto de clústeres con la ayuda del método de suma de cuadrados dentro del clústerUn clúster es un conjunto de empresas y organizaciones interconectadas que operan en un mismo sector o área geográfica, y que colaboran para mejorar su competitividad. Estos agrupamientos permiten compartir recursos, conocimientos y tecnologías, fomentando la innovación y el crecimiento económico. Los clústeres pueden abarcar diversas industrias, desde tecnología hasta agricultura, y son fundamentales para el desarrollo regional y la creación de empleo.... (WCSS).
WCSS Representa la suma de los cuadrados de las distancias de los puntos de datos en todos y cada uno de los grupos desde su centroide.
La idea principal es minimizar la distancia entre los puntos de datos y el centroide de los conglomerados. El proceso se itera hasta alcanzar un valor mínimo para la suma de distancias.
Para encontrar el valor óptimo de los clústeres, el método del codo sigue los pasos a continuación:
1 Ejecute el agrupamientoEl "agrupamiento" es un concepto que se refiere a la organización de elementos o individuos en grupos con características o objetivos comunes. Este proceso se utiliza en diversas disciplinas, incluyendo la psicología, la educación y la biología, para facilitar el análisis y la comprensión de comportamientos o fenómenos. En el ámbito educativo, por ejemplo, el agrupamiento puede mejorar la interacción y el aprendizaje entre los estudiantes al fomentar el trabajo... de K-medias en un conjunto de datos dado para diferentes valores de K (que van del 1 al 10).
2 Para cada valor de K, calcula el valor WCSS.
3 Traza un gráfico / curva entre los valores WCSS y el número respectivo de conglomerados K.
4 El punto agudo de curvatura o un punto (que parece una articulación del codo) de la trama como un brazo, se considerará como el mejor / óptimo valor de K
5. Implementación de Python
Importar bibliotecas relevantes
import numpy as np import pandas as pd import statsmodels.api as sm import matplotlib.pyplot as plt import seaborn as sns sns.set() from sklearn.cluster import KMeans
Cargando los datos
data = pd.read_csv('Countryclusters.csv')
data
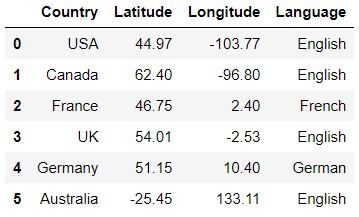
Graficar los datos
plt.scatter(data['Longitude'],data['Latitude']) plt.xlim(-180,180) plt.ylim(-90,90) plt.show()
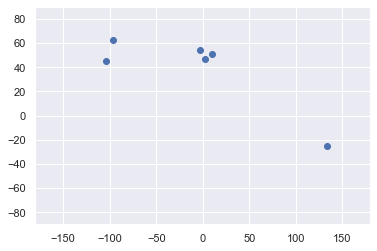
Seleccionar la función
x = data.iloc[:,1:3] # 1t for rows and second for columns x
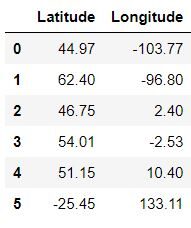
Agrupación
kmeans = KMeans(3) means.fit(x)
Resultados de la agrupación en clústeres
identified_clusters = kmeans.fit_predict(x) identified_clusters
array([1, 1, 0, 0, 0, 2])
data_with_clusters = data.copy() data_with_clusters['Clusters'] = identified_clusters plt.scatter(data_with_clusters['Longitude'],data_with_clusters['Latitude'],c=data_with_clusters['Clusters'],cmap='rainbow')
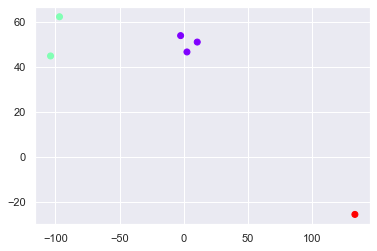
Probar un método diferente (para encontrar no. De grupos para seleccionar)
WCSS y método del codo
wcss=[]
for i in range(1,7):
kmeans = KMeans(i)
kmeans.fit(x)
wcss_iter = kmeans.inertia_
wcss.append(wcss_iter)
number_clusters = range(1,7)
plt.plot(number_clusters,wcss)
plt.title('The Elbow title')
plt.xlabel('Number of clusters')
plt.ylabel('WCSS')
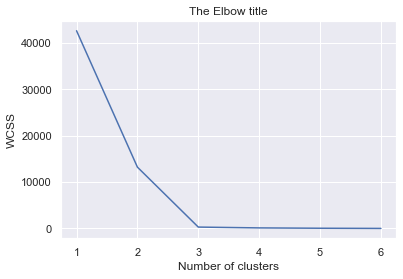
podemos elegir 3 como no. de conglomerados, este método muestra cuál es el buen número de conglomerados.
Con esto termino este blog.
Hola a todos, Namaste
Mi nombre es Pranshu Sharma y soy un entusiasta de la ciencia de datos
Muchas gracias por tomarse su valioso tiempo para leer este blog. Siéntase libre de señalar cualquier error (después de todo, soy un aprendiz) y proporcionar los comentarios correspondientes o dejar un comentario.
Dhanyvaad !!
Realimentación:
Correo electrónico: [email protected]
Los medios que se muestran en este artículo no son propiedad de DataPeaker y se utilizan a discreción del autor.
