Función de coste | Tipos de aprendizaje automático de función de costos

Este artículo fue publicado como parte del Blogatón de ciencia de datos.

Crédito: https://gifer.com/en/GxlE

Las 2 preguntas principales que surgieron en mi mente mientras trabajaba en este artículo fueron «¿Por qué estoy escribiendo este artículo?» & «¿En qué se diferencia mi artículo de otros artículos?» Bueno, la función de costo es un concepto importante de entender en los campos de la ciencia de datos, pero mientras seguía mi posgrado, me di cuenta de que los recursos disponibles en línea son demasiado generales y no cubren mis necesidades por completo.

Tuve que consultar muchos artículos y ver algunos videos en YouTube para tener una idea de las funciones de costos. Como resultado, quería reunir las funciones «Qué», «Cuándo», «Cómo» y «Por qué» de Cost que pueden ayudar a explicar este tema con mayor claridad. ¡Espero que mi artículo actúe como una ventanilla única para las funciones de costos!

Guía ficticia de la función de coste 🤷‍♀️

Función de pérdidaLa función de pérdida es una herramienta fundamental en el aprendizaje automático que cuantifica la discrepancia entre las predicciones del modelo y los valores reales. Su objetivo es guiar el proceso de entrenamiento al minimizar esta diferencia, permitiendo así que el modelo aprenda de manera más efectiva. Existen diferentes tipos de funciones de pérdida, como el error cuadrático medio y la entropía cruzada, cada una adecuada para distintas tareas y...: se utiliza cuando nos referimos al error de un solo ejemplo de entrenamientoEl entrenamiento es un proceso sistemático diseñado para mejorar habilidades, conocimientos o capacidades físicas. Se aplica en diversas áreas, como el deporte, la educación y el desarrollo profesional. Un programa de entrenamiento efectivo incluye la planificación de objetivos, la práctica regular y la evaluación del progreso. La adaptación a las necesidades individuales y la motivación son factores clave para lograr resultados exitosos y sostenibles en cualquier disciplina.....
Función de coste: se utiliza para hacer referencia a un promedio de las funciones de pérdida en un conjunto de datos de entrenamiento completo.

Pero, ¿* por qué * usar una función de costo?

¿Por qué demonios necesitamos una función de costos? Considere un escenario en el que deseamos clasificar los datos. Supongamos que tenemos los detalles de altura y peso de algunos perros y gatos. Usemos estas 2 características para clasificarlas correctamente. Si trazamos estos registros, obtenemos el siguiente diagrama de dispersiónEl diagrama de dispersión es una herramienta gráfica utilizada en estadística para visualizar la relación entre dos variables. Consiste en un conjunto de puntos en un plano cartesiano, donde cada punto representa un par de valores correspondientes a las variables analizadas. Este tipo de gráfico permite identificar patrones, tendencias y posibles correlaciones, facilitando la interpretación de datos y la toma de decisiones basadas en la información visual presentada....:

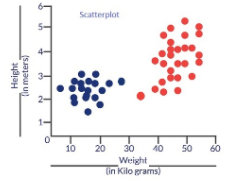
Fig 1: Diagrama de dispersión para la altura y el peso de varios perros y gatos

Los puntos azules son gatos y los puntos rojos son perros. A continuación se presentan algunas soluciones al problema de clasificación anterior.

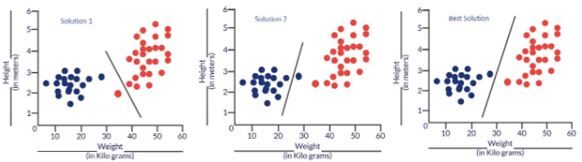
Fig: Soluciones probables a nuestro problema de clasificación

Esencialmente, los tres clasificadores tienen una precisión muy alta, pero la tercera solución es la mejor porque no clasifica erróneamente ningún punto. La razón por la que clasifica todos los puntos a la perfección es que la línea está casi exactamente entre los dos grupos y no más cerca de ninguno de los grupos. Aquí es donde entra el concepto de función de costo. La función de costo nos ayuda a alcanzar la solución óptima. La función de costo es la técnica de evaluar «el desempeño de nuestro algoritmo / modelo».

Toma tanto los resultados previstos por el modelo como los resultados reales, y calcula cuánto se equivocó el modelo en su predicción. Produce un número más alto si nuestras predicciones difieren mucho de los valores reales. A medidaLa "medida" es un concepto fundamental en diversas disciplinas, que se refiere al proceso de cuantificar características o magnitudes de objetos, fenómenos o situaciones. En matemáticas, se utiliza para determinar longitudes, áreas y volúmenes, mientras que en ciencias sociales puede referirse a la evaluación de variables cualitativas y cuantitativas. La precisión en la medición es crucial para obtener resultados confiables y válidos en cualquier investigación o aplicación práctica.... que ajustamos nuestro modelo para mejorar las predicciones, la función de costo actúa como un indicador de cómo ha mejorado el modelo. Este es esencialmente un problema de optimización. Las estrategias de optimización siempre apuntan a “minimizar la función de costes”.

Tipos de función de costes

Hay muchas funciones de costos en el aprendizaje automático y cada una tiene sus casos de uso dependiendo de si se trata de un problema de regresión o de clasificación.

1. Función de costo de regresión
2. Funciones de costo de clasificación binaria
3. Funciones de costos de clasificación de clases múltiples

1. Función de costo de regresión:

Los modelos de regresión tratan de predecir un valor continuo, por ejemplo, el salario de un empleado, el precio de un automóvil, la predicción de un préstamo, etc. Una función de costo utilizada en el problema de regresión se llama «Función de costo de regresión». Se calculan sobre el error basado en la distancia de la siguiente manera:

Error = y-y ‘

Dónde,

Y – Entrada real

Y ‘- Salida prevista

Las funciones de costo de regresión más utilizadas se encuentran a continuación,

1.1 Error medio (ME)

• En esta función de costo, se calcula el error para cada dato de entrenamiento y luego se deriva el valor medio de todos estos errores.
• Calcular la media de los errores es la forma más sencilla e intuitiva posible.
• Los errores pueden ser tanto negativos como positivos. Por lo tanto, pueden cancelarse entre sí durante la suma, lo que da un error medio cero para el modelo.
• Por lo tanto, esta no es una función de costo recomendada, pero sienta las bases para otras funciones de costo de los modelos de regresión.

1.2 Error cuadrático medio (MSE)

• Esto mejora el inconveniente que encontramos en el error medio anterior. Aquí se calcula un cuadrado de la diferencia entre el valor real y el predicho para evitar cualquier posibilidad de error negativo.
• Se mide como el promedio de la suma de las diferencias al cuadrado entre las predicciones y las observaciones reales.

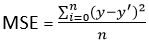
MSE = (suma de errores cuadrados) / n

• También se conoce como pérdida L2.
• En MSE, dado que cada error se eleva al cuadrado, ayuda a penalizar incluso pequeñas desviaciones en la predicción en comparación con MAE. Pero si nuestro conjunto de datos tiene valores atípicos que contribuyen a errores de predicción más grandes, entonces cuadrar este error aún más magnificará el error muchas veces más y también conducirá a un error de MSE más alto.
• Por lo tanto, podemos decir que es menos robusto a los valores atípicos.

1.3 Error absoluto medio (MAE)

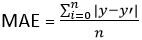
MAE = (suma de errores absolutos) / n

2. Funciones de costo para problemas de clasificación

Las funciones de costo que se usan en los problemas de clasificación son diferentes de las que usamos en el problema de regresión. Una función de pérdida comúnmente utilizada para la clasificación es la pérdida de entropía cruzada. Entendamos la entropía cruzada con un pequeño ejemplo. Considere que tenemos un problema de clasificación de 3 clases como sigue.

Clase (naranja, manzana, tomate)

El modelo de aprendizaje automático dará una distribución de probabilidad de estas 3 clases como salida para un dato de entrada dado. La clase con mayor probabilidad se considera una clase ganadora para la predicción.

Salida = [P(Orange),P(Apple),P(Tomato)]

La distribución de probabilidad real para cada clase se muestra a continuación.

Naranja = [1,0,0]

Manzana = [0,1,0]

Tomate = [0,0,1]

Si durante la fase de entrenamiento, la clase de entrada es Tomate, la distribución de probabilidad predicha debería tender hacia la distribución de probabilidad real de Tomate. Si la distribución de probabilidad predicha no se acerca más a la real, el modelo debe ajustar su peso. Aquí es donde la entropía cruzada se convierte en una herramienta para calcular qué tan lejos está la distribución de probabilidad predicha de la real. En otras palabras, la entropía cruzada se puede considerar como una forma de medir la distancia entre dos distribuciones de probabilidad. La siguiente imagen ilustra la intuición detrás de la entropía cruzada:

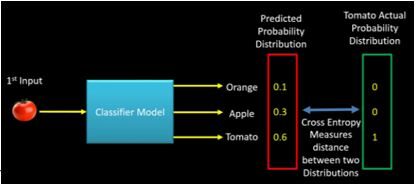
FIGURA"Figura" es un término que se utiliza en diversos contextos, desde el arte hasta la anatomía. En el ámbito artístico, se refiere a la representación de formas humanas o animales en esculturas y pinturas. En la anatomía, designa la forma y estructura del cuerpo. Además, en matemáticas, "figura" se relaciona con las formas geométricas. Su versatilidad hace que sea un concepto fundamental en múltiples disciplinas.... 3: Intuición detrás de croos-entropía (crédito – machinelearningknowledge.ai)

Esto fue solo una intuición detrás de la entropía cruzada. Tiene su origen en la teoría de la información. Ahora, con esta comprensión de la entropía cruzada, veamos ahora las funciones de costo de clasificación.

2.1 Funciones de costos de clasificación de clases múltiples

Esta función de costo se usa en los problemas de clasificación donde hay múltiples clases y los datos de entrada pertenecen a una sola clase. Entendamos ahora cómo se calcula la entropía cruzada. Supongamos que el modelo da la distribución de probabilidad como se muestra a continuación para ‘n’ clases y para un dato de entrada particular D.

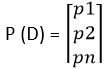
Y la distribución de probabilidad real o objetivo de los datos D es

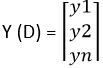
Luego, la entropía cruzada para ese dato particular D se calcula como

Pérdida de entropía cruzada (y, p) = – y^T registro (p)

= – (y₁ log (p₁) + y₂ log (p₂) + …… y_norte log (p_norte))

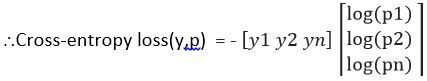
Definamos ahora la función de costo usando el ejemplo anterior (Consulte la imagen de entropía cruzada -Fig3),

p (tomate) = [0.1, 0.3, 0.6]

y (tomate) = [0, 0, 1]

Entropía cruzada (D) = – y * log (p) cuando y = 1

Entropía cruzada (D) = – (1-y) * log (1-p) cuando y = 0

Entropía cruzada binaria = (Suma de entropía cruzada para N datos) / N

Conclusión

Relacionado