Algoritmo de árbol de decisión para clasificación: aprendizaje automático 101

Este artículo fue publicado como parte del Blogatón de ciencia de datos.

Visión general

• Obtenga más información sobre el algoritmo del árbol de decisiones en el aprendizaje automático para problemas de clasificación.
• aquí hemos cubierto la entropía, la ganancia de información y la impureza de Gini

Algoritmo de árbol de decisión

algoritmos. Eso se puede utilizar tanto para un problema de clasificación como para un problema de regresión.

El objetivo de este algoritmo es crear un modelo que predice el valor de una variable objetivo, para lo cual el árbol de decisión utiliza la representación del árbol para resolver el problema en el que el nodo hoja corresponde a una etiqueta de clase y los atributos se representan en el nodo interno. del árbol.

Tomemos un conjunto de datos de muestra para avanzar más….

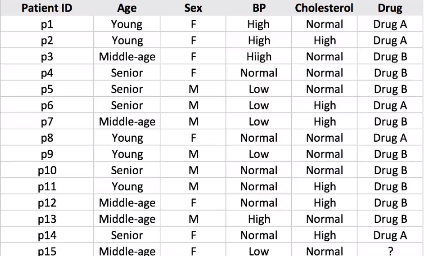
Supongamos que tenemos una muestra de 14 conjuntos de datos de pacientes y tenemos que predecir qué fármaco sugerir al paciente A o B.

Digamos que elegimos el colesterol como el primer atributo para dividir los datos

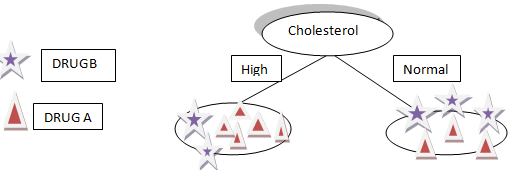
Dividirá nuestros datos en dos ramas Alto y Normal según el colesterol, como puede ver en la figura"Figura" es un término que se utiliza en diversos contextos, desde el arte hasta la anatomía. En el ámbito artístico, se refiere a la representación de formas humanas o animales en esculturas y pinturas. En la anatomía, designa la forma y estructura del cuerpo. Además, en matemáticas, "figura" se relaciona con las formas geométricas. Su versatilidad hace que sea un concepto fundamental en múltiples disciplinas.... anterior.

Supongamos que nuestro nuevo paciente tiene colesterol alto por la división anterior de nuestros datos que no podemos decir ya sea El fármaco B o el fármaco A serán adecuados para el paciente.

Además, si el colesterol del paciente es normal, todavía no tenemos una idea o información para determinar si el fármaco A o el fármaco B son adecuados para el paciente.

Tomemos Otra edad de atributo, como podemos ver, la edad tiene tres categorías: Joven, medianaLa mediana es una medida estadística que representa el valor central de un conjunto de datos ordenados. Para calcularla, se organizan los datos de menor a mayor y se identifica el número que se encuentra en el medio. Si hay un número par de observaciones, se promedia los dos valores centrales. Este indicador es especialmente útil en distribuciones asimétricas, ya que no se ve afectado por valores extremos.... edad y mayor, intentemos dividir.

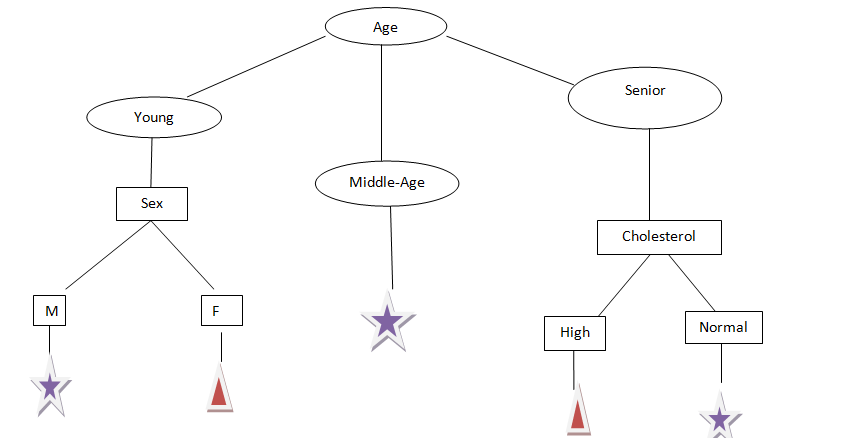
A partir de la figura anterior, ahora podemos decir que podemos predecir fácilmente qué fármaco administrar a un paciente en función de sus informes.

Supuestos que hacemos al usar el árbol de decisiones:

– Al principio, consideramos todo el conjunto de entrenamientoEl entrenamiento es un proceso sistemático diseñado para mejorar habilidades, conocimientos o capacidades físicas. Se aplica en diversas áreas, como el deporte, la educación y el desarrollo profesional. Un programa de entrenamiento efectivo incluye la planificación de objetivos, la práctica regular y la evaluación del progreso. La adaptación a las necesidades individuales y la motivación son factores clave para lograr resultados exitosos y sostenibles en cualquier disciplina.... como la raíz.

-Se prefiere que los valores de las características sean categóricos, si los valores continúan, se convierten a discretos antes de construir el modelo.

-Basado en los valores de los atributos, los registros se distribuyen de forma recursiva.

-Utilizamos un método estadístico para ordenar atributos como nodoNodo es una plataforma digital que facilita la conexión entre profesionales y empresas en busca de talento. A través de un sistema intuitivo, permite a los usuarios crear perfiles, compartir experiencias y acceder a oportunidades laborales. Su enfoque en la colaboración y el networking hace de Nodo una herramienta valiosa para quienes desean expandir su red profesional y encontrar proyectos que se alineen con sus habilidades y objetivos.... raíz o nodo interno.

Matemáticas detrás del algoritmo del árbol de decisión: Antes de pasar a la ganancia de información, primero tenemos que entender la entropía.

Entropía: Entropía son las medidas de impureza, trastorno, o incertidumbre en un montón de ejemplos.

Propósito de la entropía:

La entropía controla cómo un árbol de decisión decide separar los datos. Afecta cómo un Árbol de decisión dibuja sus límites.

“Los valores de la entropía van de 0 a 1”, menos el valor de la entropía es más confiable.

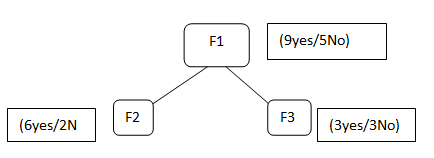
Supongamos que tenemos características F1, F2, F3, seleccionamos la característica F1 como nuestro nodo raíz

F1 contiene 9 etiqueta sí y 5 no etiqueta, después de dividir la F1 obtenemos F2 que tiene 6 sí / 2 No y F3 que tiene 3 sí / 3 no.

Ahora, si tratamos de calcular la Entropía de ambos F2 usando la fórmula de Entropía …

Poniendo los valores en la fórmula:

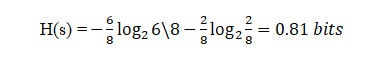
Aquí, 6 es el número de sí tomados como positivos ya que estamos calculando la probabilidad dividida por 8 es el total de filas presentes en F2.

Del mismo modo, si realizamos Entropía para F3 obtendremos 1 bit que es un caso de un atributo ya que en él hay 50%, sí y 50% no.

Esta división continuará a menos que y hasta que obtengamos un subconjunto puro.

¿Qué es un Puresubset?

El subconjunto puro es una situación en la que obtendremos todo sí o todo no en este caso.

Hemos realizado esto con respecto a un nodo, ¿y si después de dividir F2 también podemos requerir algún otro atributo para llegar al nodo hoja y también tenemos que tomar la entropía de esos valores y sumarlos para hacer el envío de todos esos valores de entropía para ese? tenemos el concepto de ganancia de información.

Ganancia de información: La ganancia de información se utiliza para decidir en qué función dividir en cada paso de la construcción del árbol. La simplicidad es lo mejor, por eso queremos que nuestro árbol sea pequeño. Para hacerlo, en cada paso debemos elegir la división que resulte en los nodos hijos más puros. Una medidaLa "medida" es un concepto fundamental en diversas disciplinas, que se refiere al proceso de cuantificar características o magnitudes de objetos, fenómenos o situaciones. En matemáticas, se utiliza para determinar longitudes, áreas y volúmenes, mientras que en ciencias sociales puede referirse a la evaluación de variables cualitativas y cuantitativas. La precisión en la medición es crucial para obtener resultados confiables y válidos en cualquier investigación o aplicación práctica.... de pureza comúnmente utilizada se llama información.

Para cada nodo del árbol, el valor de información mide cuánta información nos brinda una característica sobre la clase. La división con la mayor ganancia de información se tomará como la primera división y el proceso continuará hasta que todos los nodos secundarios sean puros o hasta que la ganancia de información sea 0.

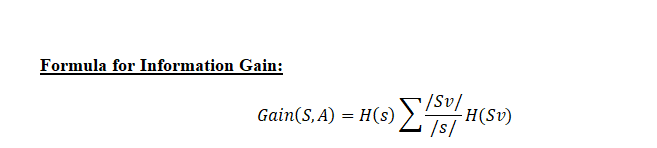
El algoritmo calcula la ganancia de información para cada división y se selecciona la división que da el valor más alto de ganancia de información.

Podemos decir que en Ganancia de información vamos a calcular el promedio de toda la entropía en función de la división específica.

Sv = Muestra total después de la división como en F2 hay 6 sí

S = Muestra total como en F1 = 9 + 5 = 14

Ahora calculando la ganancia de información:

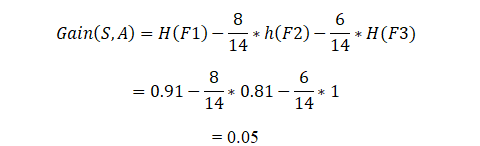
De esta manera, el algoritmo realizará esto para n número de divisiones, y la ganancia de información para la división que sea mayor la va a tomar para construir el árbol de decisión.

Cuanto mayor sea el valor de la ganancia de información de la división, mayor será la probabilidad de que se seleccione para la división en particular.

Impureza de Gini:

La impureza de Gini es una medida utilizada para construir árboles de decisión para determinar cómo las características de un conjunto de datos deben dividir los nodos para formar el árbol. Más precisamente, la impureza de Gini de un conjunto de datos es un número entre 0-0,5, lo que indica la probabilidad de que los datos nuevos y aleatorios se clasifiquen incorrectamente si se les asigna una etiqueta de clase aleatoria de acuerdo con la distribución de clases en el conjunto de datos.

Entropía vs Impureza de Gini

El valor máximo de entropía es 1, mientras que el valor máximo de impureza de Gini es 0,5.

Como el Gini Impurit

En este artículo, hemos cubierto muchos detalles sobre el árbol de decisiones, cómo funciona y las matemáticas detrás de él, medidas de selección de atributos como Entropía, Ganancia de información, Impureza de Gini con sus fórmulas y cómo lo resuelve el algoritmo de aprendizaje automático.

A estas alturas, espero que se haya hecho una idea sobre el árbol de decisiones, uno de los mejores algoritmos de aprendizaje automático para resolver un problema de clasificación.

Como nuevo, le aconsejo que aprenda estas técnicas y comprenda su implementación y luego las implemente en sus modelos.

para una mejor comprensión, consulte https://scikit-learn.org/stable/modules/tree.html

Relacionado