Algoritmo KNN | ¿Qué es el algoritmo KNN?

Visión general:

Este artículo de KNN es para:

· Comprender la representación y predicción del algoritmo de K más cercano (KNN).

· Comprender cómo elegir el valor K y la métrica de distancia.

· Métodos de preparación de datos requeridos y Pros y contras del algoritmo KNN.

· Implementación de pseudocódigo y Python.

Introducción:

K El algoritmo del vecino más cercano se incluye en la categoría de aprendizaje supervisadoEl aprendizaje supervisado es un enfoque de machine learning donde un modelo se entrena utilizando un conjunto de datos etiquetados. Cada entrada en el conjunto de datos está asociada a una salida conocida, lo que permite al modelo aprender a predecir resultados para nuevas entradas. Este método es ampliamente utilizado en aplicaciones como la clasificación de imágenes, el reconocimiento de voz y la predicción de tendencias, destacando su importancia en... y se usa para clasificación (más comúnmente) y regresión. Es un algoritmo versátil que también se utiliza para imputar valores perdidos y remuestrear conjuntos de datos. Como sugiere el nombre (K vecino más cercano), considera K vecinos más cercanos (puntos de datos) para predecir la clase o el valor continuo para el nuevo punto de datos.

El aprendizaje del algoritmo es:

1. Aprendizaje basado en instancias: aquí no aprendemos ponderaciones de los datos de entrenamientoEl entrenamiento es un proceso sistemático diseñado para mejorar habilidades, conocimientos o capacidades físicas. Se aplica en diversas áreas, como el deporte, la educación y el desarrollo profesional. Un programa de entrenamiento efectivo incluye la planificación de objetivos, la práctica regular y la evaluación del progreso. La adaptación a las necesidades individuales y la motivación son factores clave para lograr resultados exitosos y sostenibles en cualquier disciplina.... para predecir la salida (como en los algoritmos basados ​​en modelos), sino que usamos instancias de entrenamiento completas para predecir la salida de datos no vistos.

2. Aprendizaje perezoso: el modelo no se aprende utilizando datos de entrenamiento antes y el proceso de aprendizaje se pospone a un momento en el que se solicita la predicción en la nueva instancia.

3. No paramétrico: En KNN, no existe una forma predefinida de la función de mapeo.

¿Cómo funciona KNN?

1. Principio:

   Considere la siguiente figura"Figura" es un término que se utiliza en diversos contextos, desde el arte hasta la anatomía. En el ámbito artístico, se refiere a la representación de formas humanas o animales en esculturas y pinturas. En la anatomía, designa la forma y estructura del cuerpo. Además, en matemáticas, "figura" se relaciona con las formas geométricas. Su versatilidad hace que sea un concepto fundamental en múltiples disciplinas..... Digamos que hemos trazado puntos de datos de nuestro conjunto de entrenamiento en un espacio de características bidimensional. Como se muestra, tenemos un total de 6 puntos de datos (3 rojos y 3 azules). Los puntos de datos rojos pertenecen a ‘class1’ y los puntos de datos azules pertenecen a ‘class2’. Y el punto de datos amarillo en un espacio de características representa el nuevo punto para el que se va a predecir una clase. Obviamente, decimos que pertenece a ‘class1’ (puntos rojos)

   ¿Por qué?

   ¡Porque sus vecinos más cercanos pertenecen a esa clase!

   

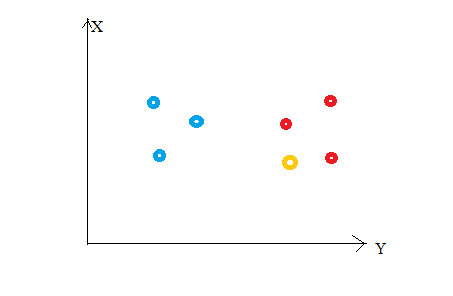
   Sí, este es el principio detrás de K Neighbors Neighbours. Aquí, los vecinos más cercanos son aquellos puntos de datos que tienen una distancia mínima en el espacio de características desde nuestro nuevo punto de datos. Y K es el número de puntos de datos que consideramos en nuestra implementación del algoritmo. Por lo tanto, la métrica de distancia y el valor K son dos consideraciones importantes al utilizar el algoritmo KNN. La distancia euclidiana es la métrica de distancia más popular. También puede utilizar la distancia de Hamming, la distancia de Manhattan, la distancia de Minkowski según sus necesidades. Para predecir clase / valor continuo para un nuevo punto de datos, considera todos los puntos de datos en el conjunto de datos de entrenamiento. Encuentra los vecinos más cercanos (puntos de datos) ‘K’ de los puntos de datos nuevos del espacio de entidades y sus etiquetas de clase o valores continuos.

   Luego:

   Para clasificación: una etiqueta de clase asignada a la mayoría de los K vecinos más cercanos del conjunto de datos de entrenamiento se considera una clase predicha para el nuevo punto de datos.

   Para regresión: la media o medianaLa mediana es una medida estadística que representa el valor central de un conjunto de datos ordenados. Para calcularla, se organizan los datos de menor a mayor y se identifica el número que se encuentra en el medio. Si hay un número par de observaciones, se promedia los dos valores centrales. Este indicador es especialmente útil en distribuciones asimétricas, ya que no se ve afectado por valores extremos.... de los valores continuos asignados a K vecinos más cercanos del conjunto de datos de entrenamiento es un valor continuo predicho para nuestro nuevo punto de datos

2. Representación del modelo
   

   Aquí, no aprendemos los pesos y los almacenamos, sino que todo el conjunto de datos de entrenamiento se almacena en la memoria. Por lo tanto, la representación del modelo para KNN es el conjunto de datos de entrenamiento completo.

¿Cómo elegir el valor de K?

K es un parámetro crucial en el algoritmo KNN. Algunas sugerencias para elegir K Value son:

1. Uso de curvas de error: la siguiente figura muestra las curvas de error para diferentes valores de K para los datos de entrenamiento y prueba.

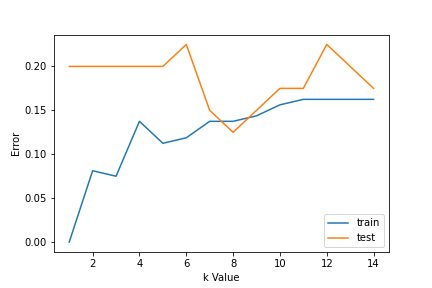
A valores bajos de K, hay sobreajuste de datos / alta varianza. Por lo tanto, el error de prueba es alto y el error de tren es bajo. En K = 1 en los datos del tren, el error siempre es cero, porque el vecino más cercano a ese punto es ese punto en sí. Por lo tanto, aunque el error de entrenamiento es bajo, el error de prueba es alto con valores de K más bajos. A esto se le llama sobreajuste. A medidaLa "medida" es un concepto fundamental en diversas disciplinas, que se refiere al proceso de cuantificar características o magnitudes de objetos, fenómenos o situaciones. En matemáticas, se utiliza para determinar longitudes, áreas y volúmenes, mientras que en ciencias sociales puede referirse a la evaluación de variables cualitativas y cuantitativas. La precisión en la medición es crucial para obtener resultados confiables y válidos en cualquier investigación o aplicación práctica.... que aumentamos el valor de K, se reduce el error de prueba.

Pero después de un cierto valor de K, se introduce sesgo / desajuste y el error de prueba aumenta. Entonces, podemos decir que inicialmente el error de los datos de prueba es alto (debido a la varianza), luego baja y se estabiliza y con un aumento adicional en el valor de K, nuevamente aumenta (debido al sesgo). El valor de K cuando el error de prueba se estabiliza y es bajo se considera el valor óptimo para K. De la curva de error anterior, podemos elegir K = 8 para la implementación de nuestro algoritmo KNN.

2. Además, el conocimiento del dominio es muy útil para elegir el valor K.

3. El valor de K debe ser impar al considerar la clasificación binaria (dos clases).

Preparación de datos requerida:

1. Escala de datos: para ubicar el punto de datos en el espacio de características multidimensionales, sería útil si todas las características están en la misma escala. Por lo tanto, la normalizaciónLa normalización es un proceso fundamental en diversas disciplinas, que busca establecer estándares y criterios uniformes para mejorar la calidad y la eficiencia. En contextos como la ingeniería, la educación y la administración, la normalización facilita la comparación, la interoperabilidad y la comprensión mutua. Al implementar normas, se promueve la cohesión y se optimizan recursos, lo que contribuye al desarrollo sostenible y a la mejora continua de los procesos.... o estandarización de los datos ayudará.

2. Reducción de dimensionalidad: KNN puede no funcionar bien si hay demasiadas funciones. Por lo tanto, se pueden implementar técnicas de reducción de dimensionalidad como la selección de características y el análisis de componentes principales.

3. Tratamiento de valor faltante: si de M características faltan datos de una característica para un ejemplo particular en el conjunto de entrenamiento, entonces no podemos ubicar o calcular la distancia desde ese punto. Por lo tanto, es necesario eliminar esa fila o imputación.

Implementación de Python:

Implementación del algoritmo del vecino más cercano K usando la biblioteca scikit-learn de Python:

Paso 1: obtener y preparar datos

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier 
from sklearn import metrics

Después de cargar bibliotecas importantes, creamos nuestros datos usando sklearn.datasets con 200 muestras, 8 características y 2 clases. Luego, los datos se dividen en el tren (80%) y los datos de prueba (20%) y se escalan usando StandardScaler.

X,Y=make_classification(n_samples= 200,n_features=8,n_informative=8,n_redundant=0,n_repeated=0,n_classes=2,random_state=14)
X_train, X_test, y_train, y_test= train_test_split(X, Y, test_size= 0.2,random_state=32)
sc= StandardScaler()
sc.fit(X_train)
X_train= sc.transform(X_train)
sc.fit(X_test)
X_test= sc.transform(X_test)
X.shape

(200, 8)

Paso 2: Encuentra el valor de K

Para elegir el valor K, usamos curvas de error y valor K con varianza óptima, y ​​el error de sesgo se elige como valor K para propósitos de predicción. Con la curva de error trazada a continuación, elegimos K = 7 para la predicción

error1= []
error2= []
for k in range(1,15):
    knn= KNeighborsClassifier(n_neighbors=k)
    knn.fit(X_train,y_train)
    y_pred1= knn.predict(X_train)
    error1.append(np.mean(y_train!= y_pred1))
    y_pred2= knn.predict(X_test)
    error2.append(np.mean(y_test!= y_pred2))
# plt.figure(figsize(10,5))
plt.plot(range(1,15),error1,label="train")
plt.plot(range(1,15),error2,label="test")
plt.xlabel('k Value')
plt.ylabel('Error')
plt.legend()

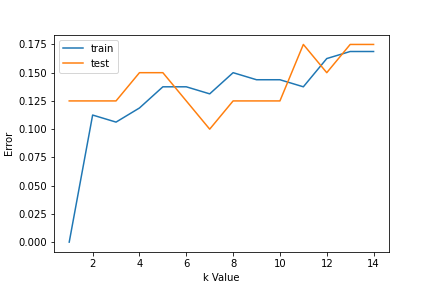
Paso 3: Predecir:

En el paso 2, hemos elegido que el valor de K sea 7. Ahora sustituimos ese valor y obtenemos la puntuación de precisión = 0,9 para los datos de la prueba.

knn= KNeighborsClassifier(n_neighbors=7)
knn.fit(X_train,y_train)
y_pred= knn.predict(X_test)
metrics.accuracy_score(y_test,y_pred)

0.9

Pseudocódigo para K vecino más cercano (clasificación):

Relacionado