Introducción
Hace tiempo, estaba haciendo el modelo predictivo usando Regresión lineal y encontré una variable cuyo coeficiente de regresión no estandarizado (beta o estimación) cercano a cero, pero después de algún análisis, encuentro que es estadísticamente significativo (significa valor p <0.05 ). Sabemos que si una variable es significativa para un modelo en particular, significa que el valor de su coeficiente es significativo y distinto de cero. Entonces, la pregunta que ocurre es "¿Por qué el valor del coeficiente es cercano a cero pero esa variable es significativa para nuestro modelo predictivo?".
La solución a esta pregunta radica en la diferencia entre los coeficientes de regresión estandarizados y no estandarizados. Entonces, en este post, veremos los conceptos básicos detrás de estos coeficientes y en qué se diferencian entre sí con sus ventajas y desventajas.
El concepto de estandarización o coeficientes estándar entra en escena cuando las variables independientes o el predictor de un modelo en particular se expresan en diferentes unidades. A modo de ejemplo, digamos que tenemos tres características independientes, a saber, altura, edad y peso. Su altura está en pulgadas, su peso en kilogramos y su edad en años. Si queremos categorizar estos predictores en función del coeficiente no estandarizado (que viene de forma directa cuando entrenamos un modelo de regresión), no sería una comparación justa puesto que las unidades para todos los predictores son diferentes.
Coeficientes de regresión no estandarizados
1. ¿Qué son los coeficientes de regresión no estandarizados?
Los coeficientes no estandarizados son aquellos que son producidos por el modelo de regresión lineal después de su entrenamiento usando las variables independientes que se miden en sus escalas originales, dicho de otra forma, en las mismas unidades en las que se toma el conjunto de datos de la fuente para entrenar el modelo.
– El coeficiente no estandarizado no debe usarse para descartar o categorizar predictores (además conocidos como variables independientes), puesto que no elimina la unidad de medida.
A modo de ejemplo, tomemos un ejemplo hipotético en el que queremos predecir los ingresos (en rupias) de una persona en función de su edad (en años), altura (en cm) y peso (en kg). Entonces, aquí las entradas para nuestro modelo de regresión son la edad, la altura y el peso, y la producción es el ingreso. Posteriormente,
Ingresos (rupias) = a0 + a1 * edad (años) + a2 * altura (cm) + a3 * peso (kg) + e (eqn-1)
2. ¿Cómo interpretar los coeficientes de regresión no estandarizados?
Se usan para interpretar el efecto de cada variable independiente sobre el resultado (respuesta / salida). Su interpretación es sencilla e intuitiva.
– Todas las demás variables se mantienen constantes, un cambio de 1 unidad en Xi (predictores) implica que hay un cambio promedio de unidades ai en Y (resultado).
En el ejemplo anterior, si a1 = 0.3, a2 = 0.2 y a3 = 0.4 (y asumimos que todos son estadísticamente significativos), entonces interpretamos estos coeficientes como:
Tener 1 año más se asocia con un incremento de 0,3 en los ingresos, asumiendo que otras variables son constantes (significa que no hay cambios en la altura y el peso).
De manera equivalente, además podemos interpretar el coeficiente para otras variables independientes.
Representa la cantidad en la que cambia la variable dependiente si cambiamos la variable independiente en una unidad manteniendo constantes las demás variables independientes.
3. Limitaciones de los coeficientes de regresión no estandarizados
– Los coeficientes no estandarizados son excelentes para interpretar la vinculación entre una variable independiente X y un resultado Y. A pesar de esto, no son útiles para comparar el efecto de una variable independiente con otra en el modelo.
– A modo de ejemplo, ¿qué variable tiene un mayor impacto en los ingresos, la edad, la estatura o el peso?
Podemos intentar responder a esta pregunta mirando la ecuación-1 y nuevamente hacerse cargo que a1 = 0.3, a2 = 0.2 y a3 = 0.4, llegamos a la conclusión de que:
«Un incremento de 20 cm de altura tiene el mismo efecto sobre el aumento de peso 10 veces»
Aún así, esto no responde a la pregunta de qué variable afecta más a la Renta.
Específicamente, la afirmación de que “el efecto del aumento de peso en 10 veces = el efecto del aumento en la altura de 20 cm” no tiene sentido sin especificar qué tan difícil es incrementar la altura en 20 cm, específicamente para alguien que no está familiarizado con esta escala.
Entonces, por último, concluimos que una comparación directa de los coeficientes de regresión para cualquiera de las dos variables independientes no tiene sentido o no es útil puesto que estas variables independientes están en las diferentes escalas (edad en años, peso en kg y talla en cm).
Resulta que los efectos de estas variables se pueden comparar usando la versión estandarizada de sus coeficientes. Y eso es lo que vamos a discutir a continuación.
Coeficientes de regresión estandarizados
1. ¿Qué son los coeficientes de regresión estandarizados?
Los coeficientes de regresión estandarizados se obtienen entrenando (o ejecutando) un modelo de regresión lineal en la forma estandarizada de las variables.
Las variables estandarizadas se calculan restando la media y dividiendo por la desviación estándar de cada observación, dicho de otra forma, calculando la puntuación Z. Haría media 0 y desviación estándar 1. Entonces, no representan sus escalas originales puesto que no disponen unidad.
Para cada observación «j» de la variable X, calculamos el puntaje z usando la fórmula:
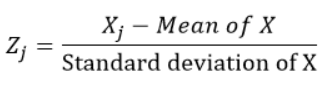
2. ¿Qué variables tenemos que estandarizar para hallar los coeficientes de regresión estandarizados, dicho de otra forma, tanto el predictor como la solución o cualquiera de ellos?
Sí, estandarizamos tanto las variables dependientes (respuesta) como las independientes (predictoras) antes de ejecutar el modelo de regresión lineal (puesto que esta es la práctica ampliamente aceptada cuando queremos hallar la forma estandarizada de las variables).
3. ¿Cómo interpretar los coeficientes de regresión estandarizados?
La interpretación de los coeficientes de regresión estandarizados no es intuitiva en comparación con sus versiones no estandarizadas:
Un cambio de 1 desviación estándar en X se asocia con un cambio de desviaciones estándar β de Y.
Nota:
– Si hay una variable categórica en lugar de una variable numérica en nuestro análisis, entonces su coeficiente estandarizado no se puede interpretar puesto que no tiene sentido cambiar X en 1 desviación estándar. En general, esto no es un obstáculo para nuestro modelo, puesto que estos coeficientes no están pensados para ser interpretados individualmente, sino para ser comparados entre sí para tener una idea de la relevancia de cada variable en el modelo de regresión lineal.
El coeficiente estandarizado se mide en unidades de desviación estándar. Un valor beta de 2.25 indica que un cambio de una desviación estándar en la variable independiente da como consecuencia un incremento de 2.25 desviaciones estándar en la variable dependiente.
4. ¿Cuál es el uso real de los coeficientes estandarizados?
Se usan principalmente para categorizar predictores (o variables independientes o explicativas) puesto que eliminan las unidades de medida de las variables independientes y dependientes). Podemos categorizar las variables independientes con un valor absoluto de coeficientes estandarizados. La variable más importante tendrá el valor absoluto máximo del coeficiente estandarizado.
A modo de ejemplo:
Y = β0 + β1 X1 + β2 X2 + ε
Si los coeficientes estandarizados β1 = 0.5 y β2 = 1, podemos concluir que:
X2 es dos veces más importante que X1 en el pronóstico de Y, suponiendo que tanto X1 y X2 siguen aproximadamente la misma distribución y sus desviaciones estándar no son tan diferentes.
5. Limitaciones de los coeficientes de regresión estandarizados
Los coeficientes estandarizados son engañosos si las variables en el modelo disponen diferentes desviaciones estándar significa que todas las variables disponen distribuciones diferentes.
Eche un vistazo a la próxima ecuación de regresión lineal:
Ingresos ($) = β0 + β1 Edad (años) + β2 Experiencia (años) + ε
Debido a que nuestras variables independientes Edad y Experiencia están en la misma escala (años) y si es razonable suponer que sus desviaciones estándar difieren mucho, entonces para este caso:
– Sus coeficientes no estandarizados deben usarse para comparar su relevancia / influencia en el modelo.
– Estandarizar estas variables haría, en realidad, que estuvieran en una escala distinto (diferentes desviaciones estándar o sigue una distribución distinto)
Cálculo de coeficientes estandarizados
1. Para regresión lineal (otro enfoque, puesto que vemos un enfoque en la parte anterior del post)
El coeficiente estandarizado se obtiene multiplicando el coeficiente no estandarizado por el motivo de las desviaciones estándar de la variable independiente y la variable dependiente.
2. Para regresión logística
Notas finales
Este post cubrió algunos conceptos básicos pero necesarios cuando trabajamos en un proyecto de la vida real en aprendizaje automático e inteligencia artificial. Espero que hayas entendido muy bien los conceptos explicados en este post. En este post en la última parte, solo vemos la formulación relacionada con los conceptos pero no profundizamos mucho sobre las Matemáticas detrás de ellos, esa parte la discutiremos en algún otro post.
Si dispones de alguna duda, ¡házmelo saber en la sección de comentarios!
Los medios que se muestran en este post no son propiedad de DataPeaker y se usan a discreción del autor.
