Preguntas de entrevistas sobre probabilidad y estadística de científicos de datos

Introducción

Las estadísticas son el corazón del aprendizaje automático

Los métodos estadísticos son clave para encontrar las respuestas a las preguntas que pretendemos adquirir a partir de los datos y son los pilares de todos los enfoques de aprendizaje automático.

En este artículo, he seleccionado una lista de 25 preguntas relacionadas con Estadística y probabilidad en ciencia de datos.

Comencemos con las Preguntas,

Sección 1

1. ¿Cuál de las siguientes relaciones es correcta para una distribución asimétrica negativa?

(a) Media = Moda = Mediana

(b) Media> Mediana> Moda

(c) Moda> Mediana> Media

(d) Media> Moda = Mediana

Solución: (c)

Explicación: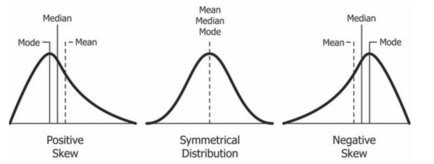

2. En la matriz de covarianza simétrica:

(a) Los elementos diagonales deben ser positivos y los demás elementos siempre son cero.

(b) Los elementos diagonales nunca pueden ser negativos y otros elementos siempre son positivos.

(c) Los elementos diagonales nunca pueden ser negativos y otros elementos pueden ser negativos o positivos.

(d) Los elementos diagonales pueden ser negativos y positivos y otros elementos son siempre negativos.

Solución: (c)

Explicación: En una matriz de covarianza, las entradas diagonales representan la covarianza de la variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... consigo misma, que es igual a la varianza de esa variable y se calcula como el cuadrado de la desviación estándar. Dado que la varianza es siempre positiva, las entradas diagonales siempre son positivas.

3. La presencia de valores atípicos en un conjunto de datos no afecta:

(a) Desviación estándar

(b) Rango

(c) Media

(d) Rango intercuartil (IQR)

Solución: (d)

Explicación: El IQR es esencialmente el rango del 50% medio de los datos. Dado que utiliza el 50% medio, no se ve afectado por los valores atípicos.

4. Si X e Y son variables aleatorias independientes, ¿cuál de las siguientes opciones es VERDADERA?

(a) E (XY) = E (X) E (Y) [ E represents Expectation value ]

(b) Cov (X, Y) = 0 [ Cov represents covariance between variables ]

(c) Var (X + Y) = Var (X) + Var (Y) [ Var represents variance ]

(Todo lo anterior

Solución: (d)

Explicación: Si X e Y son independientes, entonces Cov (X, Y) = 0 y Var (X + Y) = Var (X) + Var (Y) (∵ 2Cov (X, Y) = 0)

5. Para una distribución normal Z, ¿qué opción es VERDADERA?

(a) Coeficiente de asimetría (E (Z³)) = 0

(b) E (Z) = 0; E (Z²) = Var (Z) = 1

(c) Curtosis (E (Z⁴)) = 3

(d) Su densidad es simétrica con respecto a la media.

Solución: (d)

Explicación:

6. Sean X e Y variables aleatorias normales con sus respectivas medias 3 y 4 y varianzas 9 y 16, entonces 2X-Y tendrá distribución normal con parámetrosLos "parámetros" son variables o criterios que se utilizan para definir, medir o evaluar un fenómeno o sistema. En diversos campos como la estadística, la informática y la investigación científica, los parámetros son fundamentales para establecer normas y estándares que guían el análisis y la interpretación de datos. Su adecuada selección y manejo son cruciales para obtener resultados precisos y relevantes en cualquier estudio o proyecto....:

(a) Media = 2 y Varianza = 52

(b) Media = 0 y varianza = 1

(c) Media = 2 y Varianza = 1

(re. Ninguna de las anteriores

Solución: (d)

Insinuación: Var(hacha + bY) = a² Var(X) + b² Var(Y) + 2abCov (X, Y)

7. Suponga que X e Y toman valores {0,1} y son independientes con P (X = 1) = 1/2 y P (Y = 1) = 1/3. ¿Cuál es la probabilidad de que P (X + Y = 1)?

(a) 18/5

(b) 1/2

(c) 5/6

(d) 1/6

Solución: (b)

Explicación: P (X + Y = 1) = P (X = 0) .P (Y = 1) + P (X = 1) .P (Y = 0) = (1/2) (1/3) + (1/2) (2/3) = 1/2.

8. Sean X e Y variables aleatorias con E (X) = μ / 2 y E (Y) = μ, entonces, ¿cuál es VERDADERA?

(a) g = X + Y es un estimadorEl "Estimador" es una herramienta estadística utilizada para inferir características de una población a partir de una muestra. Se basa en métodos matemáticos para proporcionar estimaciones precisas y confiables. Existen diferentes tipos de estimadores, como los insesgados y los consistentes, que se eligen según el contexto y el objetivo del estudio. Su correcto uso es fundamental en investigaciones científicas, encuestas y análisis de datos.... insesgado de μ

(b) g = X + Y es un estimador sesgado de μ con sesgo igual a μ

(c) h = X + (Y / 2) es un estimador insesgado de μ

(d) h = X + (Y / 2) es un estimador sesgado de μ con sesgo igual a μ / 2

Solución: (c)

Explicación: E (g) = E (X + Y) = E (X) + E (Y) = 3μ / 2; Sesgo (g) = E (g) -μ = μ / 2
E (h) = E (X + (Y / 2)) = E (X) + 1 / 2E (Y) = μ, Sesgo (h) = E (h) -μ = 0

9. Suponga que X toma valores entre 0 y 1 y tiene la función de densidad de probabilidad (PDF) 2x, entonces el valor de la varianza de X² es :

(a) 1/12

(b) 1/18

(c) 1/6

(d) 18/5

Solución: (a)

Sugerencia: use Var (X²) = E (X⁴) -(EX²))²

10. Para las variables aleatorias X e Y, tenemos Var (X) = 1, Var (Y) = 4 y Var (2X-3Y) = 34, entonces la correlación entre X e Y es:

(a) 1/2

(b) 1/4

(c) 1/3

(re. Ninguna de las anteriores

Solución: (b)

Explicación: Var (2X-3Y) = 34

= 4Var (X) + 9Var (Y) -12Cov (X, Y)

= 4 (1) +9 (4) -12Cov (X, Y) = 34

∴ Cov (X, Y) = 1/2

11. Se lanza un dado regular repetidamente hasta que se observa un número mayor que 4. Si K es el número total de veces que se lanza el dado, entonces P (K = 4) es igual a:

(a) 16/81

(b) 8/81

(c) 27/8

(d) 16/27

Solución: (b)

Explicación: P (K = 4) = (P (# menos de 4 o igual))³.P ({4}) = (2/3)³. (1/3) = 8/81.

12. Sean X e Y variables aleatorias uniformes e independientes (0, 1). Defina A = X + Y y B = XY. Luego,

(a) A y B son variables aleatorias independientes

(b) A y B son variables aleatorias no correlacionadas

(c) A y B son variables aleatorias uniformes (0,1).

(d) Ninguno de estos

Solución: (b)

Explicación: Cov (X + Y, XY) = Cov (X, X) – Cov (X, Y) + Cov (Y, X) – Cov (Y, Y) ⇒ Var (X) – Var (Y) = 0

13. Si g es un estimador puntual de X, entonces el error cuadrático medio (MSE) para g es:

(a) Varianza (g) + Sesgo (g)

(b) Varianza (g) + Sesgo (g²)

(c) Varianza (g) + (Sesgo (g))²

(d) Varianza (g²) + Sesgo (g)

Solución: (c)

Explicación: MSE (g) = E[ (g-X)² ] = Var (gX) + (E[ g-X ])² = Var (g) + (Sesgo (g))²

14. Sean X e Y dos variables aleatorias y sean a, b, c, d números reales, entonces ¿cuál de los siguientes es FALSO?

(a) Cov (X + b, Y + d) = Cov (X, Y)

(b) Cov (aX, cY) = ac * Cov (X, Y)

(c) Cov (aX + b, cY + d) = ac * Cov (X, Y)

(d) Corr (aX + b, cY + d) = ac * Corr (X, Y) para a, c> 0

Solución: (d)

Explicación: Corr (aX + b, cY + d) = Corr (X, Y)

15. Sean X e Y conjuntamente (bivariados) normales con Var (X) = Var (Y), entonces:

(a) X + Y y XY son conjuntamente normales

(b) X + Y y XY no están correlacionados

(c) X + Y y XY son independientes

(Todo lo anterior

Solución: (d)

Explicación: Si X e Y son la distribución normal bivariada, entonces cualquier combinación lineal de X e Y también se distribuye normalmente.

16. Sea X₁, X₂, X₃, —, X_norte ser una muestra aleatoria de una distribución con E (X_I) =μ y Var (X_I) =.σ² Ahora, considere dos estimadores:

gramo₁= X₁ gramo₂= X ‘= (X₁+ X₂+ X₃+ ————- X_norte)/norte

¿Cuál de estos estimadores tiene un error cuadrático medio (MSE) alto?

(a) g₁

(b) g₂

(c) Lo mismo para ambos g₁ y G₂

(re. Ninguna de las anteriores

Solución: (a)

Explicación: MSE (g₁) = E[(g₁–μ)²] = E[(X₁-E(X₁))²] = Var (X₁) = σ²

MSE (g₂) = E[(g₂–μ)²]= E[(X’-μ)²] = Var (X’-μ) + (E[X’-μ])² = Var (X ‘) = σ²/norte

17. Una muestra aleatoria de n = 6 tomada de la población tiene los elementos 6, 10, 13, 14, 18, 20. Entonces, ¿qué opción es Falsa?

(a) La estimación puntual de la media poblacional es 13,5

(b) La estimación puntual de la desviación estándar de la población es 4,68

(c) La estimación puntual de la desviación estándar de la población es 3,5

(d) La estimación puntual del error estándar de la media es 1,91

Solución: (c)

Explicación: Media poblacional (X ‘) = (Σ X_I/ n) = 13,5

Desviación estándar de la población (S) = sqrt ((Σ X_I²/ n) – (Σ X_I/norte)² ) = 4,68

Error estándar de la media = S / sqrt (n) = 4.68 / sqrt (6) = 1.91

Sección 2

18. Verdadero o falso: si la correlación de Pearson entre 2 variables es cero, entonces son necesariamente independientes.

Solución: Falso

Explicación: La correlación es una medidaLa "medida" es un concepto fundamental en diversas disciplinas, que se refiere al proceso de cuantificar características o magnitudes de objetos, fenómenos o situaciones. En matemáticas, se utiliza para determinar longitudes, áreas y volúmenes, mientras que en ciencias sociales puede referirse a la evaluación de variables cualitativas y cuantitativas. La precisión en la medición es crucial para obtener resultados confiables y válidos en cualquier investigación o aplicación práctica.... de dependencia lineal entre las variables.

19. Verdadero o falso: Sea g un estimador insesgado de X y U una variable aleatoria con medias cero, entonces h = g + U también es imparcial para X.

Solución: Verdadero.

Explicación: E (h) = E (g) + E (U) = 0 + 0 = 0 ( ∵ E (g) = 0 debido al estimador insesgado)

20. Verdadero o falso: Sean X e Y dos variables aleatorias normales estándar independientes y T = XY²+ X + 1 y P = X-3, luego Cov (T, P) = 1

Solución: Falso.

Sugerencia: Utilice las propiedades mencionadas en la Pregunta 14.

21. Verdadero o falso: Sea X tiene una distribución normal con parámetros μ y σ², luego X² sigue una distribución de chi-cuadrado con el parámetro 1.

Solución: Falso.

Explicación: Para que la declaración dada sea verdadera, X debe ser una distribución normal estándar (μ = 0, σ²= 1)

22. Verdadero o Falso: Si existe la función característica de una variable aleatoria, entonces también existirá su expectativa y varianza.

Solución: Falso.

Sugerencia: función generadora de momentos (MGF)

23. Verdadero o falso: Sea X tiene una distribución uniforme U (a, b) tal que E (X) = 2 y Var (X) = 3/4, entonces P (X <1) = 1/6.

Solución: Verdadero.

Explicación: E (X) = (a + b) / 2 = a + b = 4; Var (X) = (ba)²/ 12 = (ba) = 3 ⇒ X~ U (0,5, 3,5)

24. Verdadero o falso: El coeficiente de correlación entre X + Y y XY, donde X e Y son variables aleatorias independientes con varianzas 36 y 16, respectivamente, es 6/13.

Solución: Falso.

Explicación: Corr (X + Y, XY) = Cov (X + Y, XY) / Std (X + Y) .Std (XY) [Std= Standard Deviation]

25. Verdadero o falso: en la estimación de intervalo, A medida que aumenta el nivel de confianza, el margenEl margen es un término utilizado en diversos contextos, como la contabilidad, la economía y la impresión. En contabilidad, se refiere a la diferencia entre los ingresos y los costos, lo que permite evaluar la rentabilidad de un negocio. En el ámbito editorial, el margen es el espacio en blanco alrededor del texto en una página, que facilita la lectura y proporciona una presentación estética. Su correcta gestión es esencial... de error disminuye.

Solución: Falso.

Explicación: El intervalo de confianza se define como X ± Z (s/√n)

Notas finales

¡Gracias por leer!

Espero que hayan disfrutado de las preguntas y hayan podido poner a prueba sus conocimientos sobre estadística y probabilidad en la ciencia de datos.

Si le gustó esto y desea saber más, visite mis otros artículos sobre ciencia de datos y aprendizaje automático haciendo clic en el enlace

No dude en ponerse en contacto conmigo en Linkedin, Correo electrónico.

¿Algo no mencionado o quieres compartir tus pensamientos? No dude en comentar a continuación y me pondré en contacto con usted.

Sobre el Autor

Chirag Goyal

Actualmente, estoy cursando mi Licenciatura en Tecnología (B.Tech) en Ciencias de la Computación e Ingeniería de la Instituto Indio de Tecnología de Jodhpur (IITJ). Estoy muy entusiasmado con el aprendizaje automático, el aprendizaje profundoEl aprendizaje profundo, una subdisciplina de la inteligencia artificial, se basa en redes neuronales artificiales para analizar y procesar grandes volúmenes de datos. Esta técnica permite a las máquinas aprender patrones y realizar tareas complejas, como el reconocimiento de voz y la visión por computadora. Su capacidad para mejorar continuamente a medida que se le proporcionan más datos la convierte en una herramienta clave en diversas industrias, desde la salud... y la inteligencia artificial.

Relacionado