Dieser Artikel wurde im Rahmen der Data Science Blogathon.
Überblick
K-Means-Clustering ist ein sehr bekannter und leistungsstarker unüberwachter maschineller Lernalgorithmus. Wird verwendet, um viele komplexe Probleme des unüberwachten maschinellen Lernens zu lösen. Bevor es losgeht, Schauen wir uns die Punkte an, die wir verstehen werden.
Inhaltsverzeichnis
- Einführung
- Wie funktioniert der K-Means-Algorithmus?
- So wählen Sie den Wert von K?
- Ellbogenmethode.
- Silhouette-Methode.
- Vorteile von k-means.
- Nachteile von k-means.
Einführung
Lassen Sie uns den Algorithmus von GruppierungDas "Gruppierung" Es handelt sich um ein Konzept, das sich auf die Organisation von Elementen oder Individuen in Gruppen mit gemeinsamen Merkmalen oder Zielen bezieht. Dieses Verfahren wird in verschiedenen Disziplinen eingesetzt, einschließlich Psychologie, Pädagogik und Biologie, um die Analyse und das Verständnis von Verhaltensweisen oder Phänomenen zu erleichtern. Im Bildungsbereich, zum Beispiel, Gruppenbildung kann die Interaktion und das Lernen unter den Schülern verbessern, indem sie die Arbeit fördert.. von K-Means mit seiner einfachen Definition.
Ein K-Means-Clustering-Algorithmus versucht, ähnliche Elemente in Form von Clustern zu clustern. Die Anzahl der Gruppen wird durch K . dargestellt.
Nehmen wir ein Beispiel. Angenommen, Sie gehen in einen Gemüseladen, um Gemüse zu kaufen. Dort siehst du verschiedene Gemüsesorten. Das einzige, was Sie dort bemerken werden, ist, dass das Gemüse in einer Gruppe seiner Sorten angeordnet wird. Da alle Karotten an einem Ort bleiben, Kartoffeln bleiben bei ihren Sorten und so weiter. Wenn du es hier merkst, dann werden Sie feststellen, dass sie eine Gruppe oder Gruppe bilden, wo jedes Gemüse innerhalb seiner Art der Gruppe gehalten wird, die die Gruppen bildet.
Jetzt werden wir dies mit Hilfe eines schönen verstehen. Abbildung"Abbildung" ist ein Begriff, der in verschiedenen Zusammenhängen verwendet wird, Von der Kunst zur Anatomie. Im künstlerischen Bereich, bezieht sich auf die Darstellung menschlicher oder tierischer Formen in Skulpturen und Gemälden. In der Anatomie, bezeichnet die Form und Struktur des Körpers. Was ist mehr, in der Mathematik, "Abbildung" Es hängt mit geometrischen Formen zusammen. Seine Vielseitigkeit macht es zu einem grundlegenden Konzept in mehreren Disziplinen.....
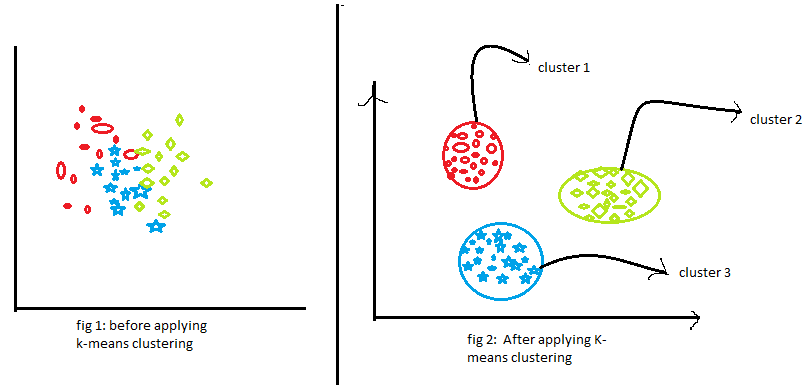
Jetzt, schau dir die beiden Abbildungen oben an. Was hast du beobachtet? Lass uns über die erste Figur sprechen. Die erste Abbildung zeigt die Daten vor der Anwendung des k-Means-Clustering-Algorithmus. Hier sind die drei verschiedenen Kategorien chaotisch. Wenn Sie diese Daten in der realen Welt sehen, Sie werden die verschiedenen Kategorien nicht herausfinden können.
Jetzt, schau dir die zweite figur an (Abbildung 2). Dies zeigt die Daten nach Anwendung des K-Means-Clustering-Algorithmus. Sie können sehen, dass die drei verschiedenen Elemente in drei verschiedene Kategorien eingeteilt sind, die als Gruppen bezeichnet werden.
Wie funktioniert der K-Means-Clustering-Algorithmus?
K-bedeutet Gruppierung versucht, ähnliche Arten von Elementen in Form von Gruppierungen zu gruppieren. Finden Sie die Ähnlichkeit zwischen den Elementen und gruppieren Sie sie in Gruppen. Der K-Means-Clustering-Algorithmus funktioniert in drei Schritten. Mal sehen, was diese drei Schritte sind.
- Wählen Sie die k-Werte.
- Initialisieren Sie die Schwerpunkte.
- Wähle die Gruppe aus und finde den Durchschnitt.
Lassen Sie uns die obigen Schritte mit Hilfe der Abbildung verstehen, denn ein gutes Bild ist besser als Tausende von Worten.
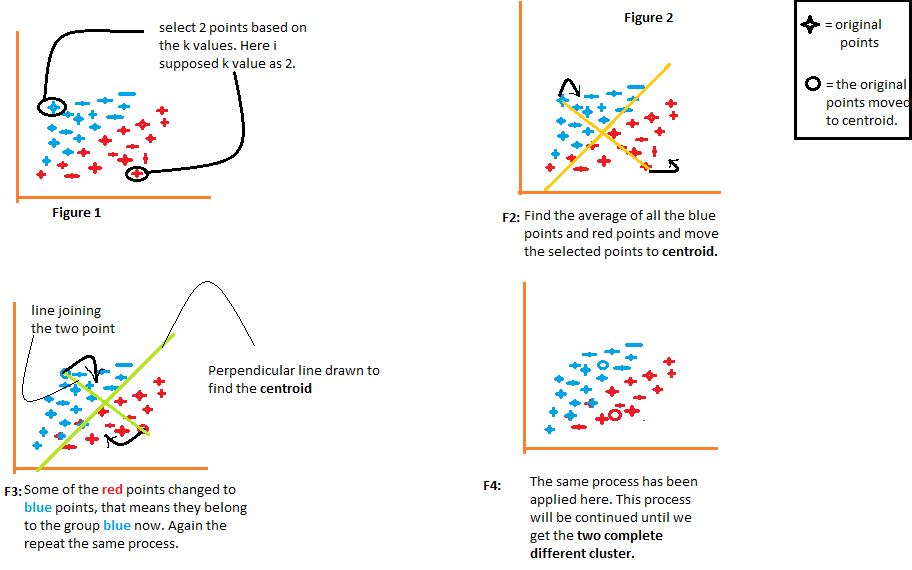
Wir werden jede Figur einzeln verstehen.
- Die Figur 1 zeigt die Datendarstellung zweier unterschiedlicher Elemente. das erste Element wird blau und das zweite Element wird rot angezeigt. Hier wähle ich den Wert von K zufällig als 2. Es gibt verschiedene Methoden, mit denen wir die richtigen k-Werte auswählen können.
- In der Figur 2, verbinden Sie die beiden ausgewählten Punkte. Jetzt, um den Schwerpunkt zu finden, wir werden eine Linie senkrecht zu dieser Linie ziehen. Punkte werden zu ihrem Schwerpunkt verschoben. Wenn du dort schaust, Sie werden sehen, dass sich einige der roten Punkte jetzt zu den blauen Punkten bewegen. Jetzt, diese Punkte gehören zur Gruppe der blauen Elemente.
- Der gleiche Vorgang wird in der Abbildung fortgesetzt 3. Wir verbinden die beiden Punkte und ziehen eine senkrechte Linie dazu und finden den Schwerpunkt. Jetzt bewegen sich die beiden Punkte zu ihrem Schwerpunkt und wieder werden einige der roten Punkte zu blauen Punkten.
- Der gleiche Vorgang findet in der Abbildung statt 4. Dieser Prozess wird so lange fortgesetzt, bis wir zwei völlig unterschiedliche Gruppen dieser Gruppen erhalten.
HINWEIS: Beachten Sie, dass die Gruppierung von K-Mitteln die euklidische Distanzmethode verwendet, um den Abstand zwischen den Punkten zu ermitteln.
Im Internet finden Sie viele Erklärungen zur euklidischen Distanz.
So wählen Sie den Wert von K?
Eine der schwierigsten Aufgaben dieses Clustering-Algorithmus ist die Auswahl der richtigen Werte von k. Was sollte der richtige k-Wert sein?? So wählen Sie den k-Wert? Lass uns die Antwort auf diese Fragen finden. Wenn Sie die k-Werte zufällig wählen, es kann richtig oder falsch sein. Wenn Sie den falschen Wert wählen, wirkt sich direkt auf die Leistung Ihres Modells aus. Dann, Es gibt zwei Methoden, mit denen Sie den richtigen Wert von k . auswählen können.
- Ellbogenmethode.
- Silhouette-Methode.
Jetzt, Lassen Sie uns beide Konzepte nacheinander im Detail verstehen.
Ellbogenmethode
Ellenbogen ist eine der bekanntesten Methoden, mit der Sie den richtigen Wert von k auswählen und die Leistung Ihres Modells steigern können. Wir führen auch Hyperparameter-Tuning durch, um den besten Wert von k . zu wählen. Mal sehen, wie diese Ellbogenmethode funktioniert.
Es ist eine empirische Methode, um den besten Wert von k . zu finden. sammle den Wertebereich und nimm das Beste davon. Berechnen Sie die Summe der Quadrate der Punkte und berechnen Sie den mittleren Abstand.
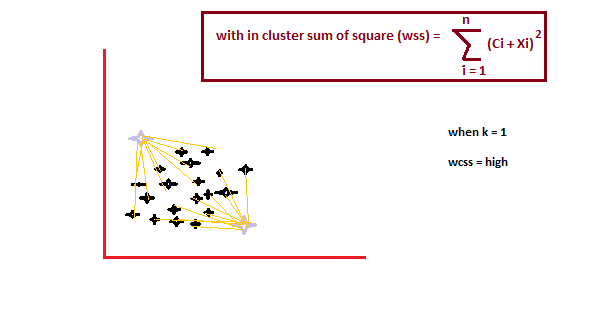
Wenn der Wert von k ist 1, die Summe der Quadrate innerhalb der Gruppe ist hoch. EIN messenDas "messen" Es ist ein grundlegendes Konzept in verschiedenen Disziplinen, , die sich auf den Prozess der Quantifizierung von Eigenschaften oder Größen von Objekten bezieht, Phänomene oder Situationen. In Mathematik, Wird verwendet, um Längen zu bestimmen, Flächen und Volumina, In den Sozialwissenschaften kann es sich auf die Bewertung qualitativer und quantitativer Variablen beziehen. Die Messgenauigkeit ist entscheidend, um zuverlässige und valide Ergebnisse in der Forschung oder praktischen Anwendung zu erhalten.... Das erhöht den Wert von K, die Summe der quadrierten Werte innerhalb der Gruppe wird kleiner.
Schließlich, Wir zeichnen eine Grafik zwischen den k-Werten und der Summe des Quadrats innerhalb der Gruppe, um den k-Wert zu erhalten. Wir werden das Diagramm sorgfältig prüfen. Irgendwann, unser Graph wird abrupt abnehmen. Dieser Punkt wird als Wert von k . betrachtet.
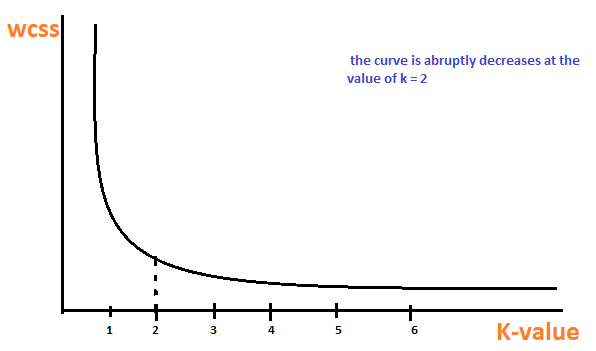
Silhouette-Methode
Die Silhouettenmethode ist etwas anders. Die Ellenbogenmethode nimmt auch den Bereich der k-Werte und zeichnet den Silhouettengraphen. Berechnen Sie den Silhouettenkoeffizienten jedes Punktes. Ermitteln Sie die durchschnittliche Entfernung von Punkten innerhalb Ihrer Gruppe zu (ich) und der durchschnittliche Abstand der Punkte zu ihrer nächstgelegenen Gruppe namens b (ich).

Notiz: Die A (ich) Wert muss kleiner als b . sein (ich) Wert, was ist ai << mit einem.
Jetzt, wir haben die Werte von a (ich) und B (ich). Wir berechnen den Silhouettenkoeffizienten mit der folgenden Formel.
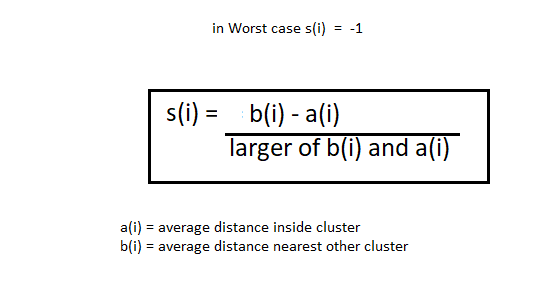
Jetzt, wir können den Silhouettenkoeffizienten aller Punkte in den Gruppen berechnen und den Silhouettengraphen zeichnen. Dieses Diagramm ist auch nützlich, um Ausreißer zu erkennen. Die Handlung der Silhouette liegt zwischen -1 ein 1.
Beachten Sie, dass für den Silhouettenkoeffizienten gleich -1 ist der schlimmste fall.
Schauen Sie sich die Grafik an und überprüfen Sie, welcher der k-Werte am nächsten ist 1.
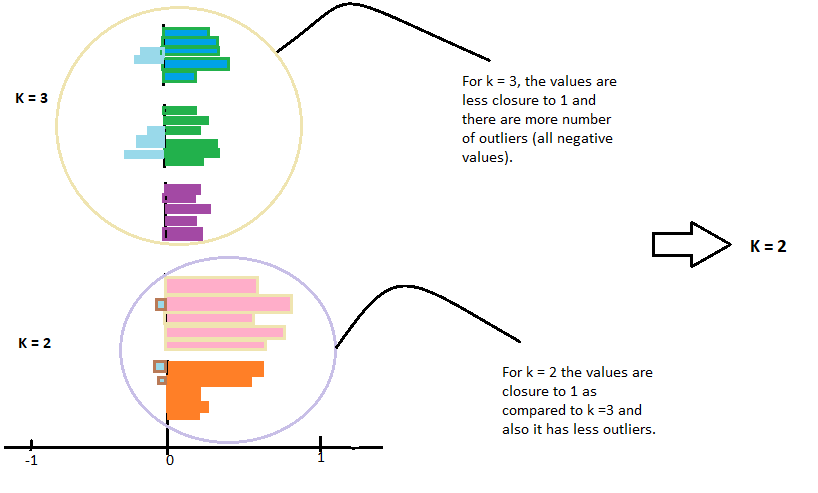
Was ist mehr, Überprüfen Sie das Diagramm mit den wenigsten Ausreißern, was ein weniger negativer Wert bedeutet. Wählen Sie dann diesen Wert von k für Ihr Modell, um es abzustimmen.
Vorteile von K-Mitteln
- Es ist sehr einfach zu implementieren.
- Es ist auf einen großen Datensatz skalierbar und auch schneller auf große Datensätze.
- sehr oft neue Beispiele anpassen.
- Verallgemeinerung von Clustern für verschiedene Formen und Größen.
Nachteile von K-Mitteln
- Es reagiert empfindlich auf Ausreißer.
- K-Werte manuell zu wählen ist harte Arbeit.
- Mit zunehmender Anzahl von Dimensionen, seine Skalierbarkeit nimmt ab.






