This article was published as part of the Data Science Blogathon
Agenda
We have all built a logistic regression at some point in our lives.. Even if we have never built a model, we have definitely learned this predictive model technique theoretically. Two simple and underappreciated concepts used in the preprocessing step to build a logistic regression model are weight of evidence and value of information.. I would like to bring you back into the spotlight through this article..
This article is structured as follows:
- Introduction to logistic regression
- Importance of Feature Selection
- Need for a good imputator for categorical features
- AFFLICTION
- IV
Let us begin!
1. Introduction to logistic regression
The first is the first, we all know that logistic regression is a classification problem. In particular, we consider here binary classification problems.
Logistic regression models take both categorical and numerical data as input and output the probability of occurrence of the event..
Examples of problem statements that can be solved with this method are:
- Given customer data, What is the probability that the customer will buy a new product presented by a company?
- Given the required data, What is the probability that a bank customer will default on a loan??
- Given the meteorological data of the last month, what is the probability that it will rain tomorrow?
All the above statements had two results. (buy and don't buy, default and non-default, rain and not rain). Therefore, a binary logistic regression model can be built. Logistic regression is a parametric method. What does this mean? A parametric method has two steps.
1. First, we assume a form or functional form. In the case of logistic regression, we assume that

2. We need to predict the weights / bi coefficients so that, the probability of an event for an observation x is close to 1 if the actual value of the target is 1 and the probability is close to 0 if the actual value of the target is 0.
With this basic understanding, let's understand why we need feature selection.
2. Importance of Feature Selection
In this digital age, we are equipped with a huge amount of data. But nevertheless, not all functions available to us are useful in all model predictions. We've all heard the saying, "Garbage in!, garbage comes out!”. Therefore, Choosing the right features for our model is of paramount importance.. Features are selected based on the predictive strength of the feature.
For instance, Let's say we want to predict the probability that a person will buy a new chicken recipe at our restaurant.. If we have a function: “Food preference” with values {Vegetarian, Not vegetarian, Eggetarian}, we are almost certain that this feature will clearly separate people who are more likely to buy this new dish from those who will never buy it. . Therefore, this feature has high predictive power.
We can quantify the predictive power of a feature using the concept of information value that will be described here..
3. Need for a good imputator for categorical functions
Logistic regression is a parametric method that requires us to compute a linear equation. This requires all features to be numeric. But nevertheless, we may have categorical features in our data sets that are nominal or ordinal. There are many imputation methods such as one-hot coding or simply assigning a number to each class of categorical features. each of these methods has its own merits and demerits. But nevertheless, I will not discuss the same here.
In the case of logistic regression, we can use the WoE concept (Weight of Evidence) to impute categorical characteristics.
4. weight of evidence
After all the background provided, We finally got to the topic of the day!!
The formula for calculating the weight of evidence for any characteristic is given by
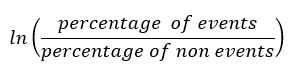
Before continuing to explain the intuition behind this formula, let's take a fictitious example:
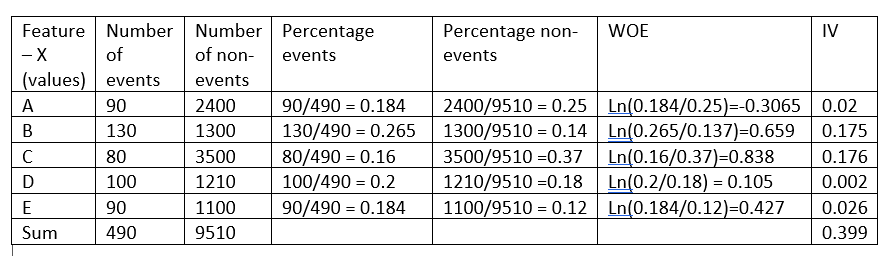
The weight of evidence indicates the predictive power of a single characteristic relative to its independent characteristic.. If any of the categories / bins of a feature have a large proportion of events compared to the proportion of non-events, we'll get a high WoE value which in turn says that that feature class separates events from non-events. .
For instance, consider category C of characteristic X in the example above, the proportion of events (0,16) is very small compared to the proportion of non-events (0,37). This implies that if the value of the characteristic X is C, the target value is more likely to be 0 (no event). The WoE value only tells us how confident we are that the function will help us correctly predict the probability of an event..
Now that we know that WoE measures the predictive power of each bin / category of a feature, what are the other benefits of WoE?
1. The WoE values for the various categories of a categorical variable can be used to impute a categorical feature and convert it to a numeric feature, since a logistic regression model requires all of its features to be numeric.
By carefully examining the WoE formula and the logistic regression equation to be solved, we see that WoE of a feature has a linear relationship with the logarithmic probabilities. This ensures that the requirement that the features have a linear relationship with the logarithmic probabilities is satisfied..
2. For the same reason as above, if a continuous feature does not have a linear relationship with the log probabilities, the feature can be grouped into groups and a new feature created by replacing each container with its WoE value can be used instead of the original feature. Therefore, WoE is a good variable transformation method for logistic regression.
3. When arranging a numeric feature in ascending order, if the WoE values are all linear, we know that the feature has the correct linear relationship with the target. But nevertheless, if the WoE of the characteristic is not linear, we should discard it or consider some other variable transformation to ensure linearity. Therefore, WoE gives us a tool to verify the linear relationship with the dependent feature.
4. WoE is better than one-hot encoding since one-hot encoding will need you to create new h-1 features to accommodate a categorical feature with h-categories. This implies that the model will not have to predict coefficients h-1 (with a) instead of 1. But nevertheless, in the transformation of the WoE variable, we will need to compute a unique coefficient for the feature under consideration.
5. Information value
Having discussed the WoE value, the WoE value tells us the predictive power of each bin of a feature. But nevertheless, a single value representing the predictive power of the entire feature will be useful in feature selection.
The equation for IV is
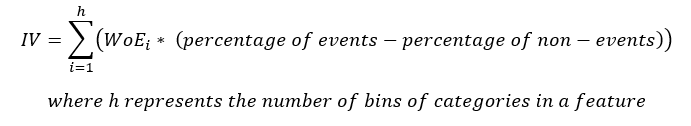
Note that the term (percentage of events – the percentage of non-events) follows the same sign as WoE, Thus, makes sure that the IV is always a positive number.
How do we interpret the value of IV?
The table below gives you a set rule to help you select the best features for your model.
| Information value | power of prediction |
| <0.02 | Useless |
| 0,02 until 0,1 | weak predictors |
| 0,1 until 0,3 | mean predictors |
| 0,3 until 0,5 | Strong predictors |
| > 0,5 | Suspicious |
As seen in the example above, feature X has an information value of 0.399, which makes it a strong predictor and, Thus, will be used in the model.
6. Conclution
As seen in the example above, WoE and IV calculation are beneficial and help us analyze multiple points as listed below.
1. WoE helps verify the linear relationship of a feature with its dependent feature to be used in the model.
2. WoE is a good variable transformation method for continuous and categorical features.
3. WoE is better than hot encoding, since this method of transformation of variables does not increase the complexity of the model.
4. IV is a good measure of the predictive power of a feature and also helps pinpoint the suspicious feature.
Although WoE and IV are very useful, always make sure it is only used with logistic regression. Unlike other feature selection methods available, features selected by IV may not be the best set of features for nonlinear model building.
I hope this article has helped you understand how WoE and IV work..
The media shown in this article is not the property of DataPeaker and is used at the author's discretion.






