Cet article a été publié dans le cadre du Blogathon sur la science des données.
introduction
Dans le post précédent, nous définissons les distributions de probabilité et discutons brièvement des différentes distributions de probabilité discrètes. Dans ce billet, nous continuerons à en apprendre davantage sur les distributions de probabilité à travers des distributions de probabilité continues.
Définition
Si vous vous souvenez de notre discussion précédente, les variables aléatoires continues peuvent prendre un nombre infini de valeurs dans un intervalle donné. Par exemple, dans l'intervalle [2, 3] il y a des valeurs infinies entre 2 Oui 3. Les distributions continues sont définies par les fonctions de densité de probabilité (PDF) au lieu de fonctions de masse de probabilité. La probabilité qu'une variable aléatoire continue soit égale à une valeur exacte est toujours nulle. Les probabilités continues sont définies sur un intervalle. Par exemple, P (X = 3) = 0 mais P (2.99 <X <3.01) peut être calculé en intégrant le PDF sur l'intervalle [2.99, 3.01]
Liste des distributions de probabilité continues
Ensuite, nous analysons les distributions de probabilités continues les plus utilisées:
1. Distribution uniforme continue
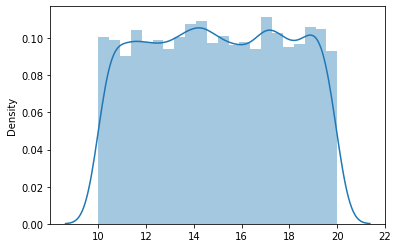
La distribution uniforme a des formes continues et discrètes. Ici, nous discutons du continuum. Cette distribution trace les variables aléatoires dont les valeurs sont également susceptibles de se produire. L'exemple le plus courant est de lancer un dé équitable. Ici, Les 6 les résultats sont tout aussi susceptibles de se produire. Pourtant, la probabilité est constante.
Prenons l'exemple où a = 10 et b = 20, la mise en page ressemble à ceci:
Le PDF est donné par,
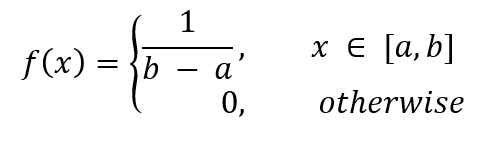
où a est la valeur minimale et b est la valeur maximale.
2. Distribution normale
C'est la distribution la plus discutée et la plus fréquemment trouvée dans le monde réel.. De nombreuses distributions continues atteignent souvent une distribution normale avec un échantillon suffisamment grand. Cela a deux paramètres, a savoir, l'écart type et la moyenne.
Cette distribution a de nombreuses propriétés intéressantes. La moyenne a la probabilité la plus élevée et toutes les autres valeurs sont également réparties des deux côtés de la moyenne de manière symétrique. La distribution normale standard est un cas particulier où la moyenne est 0 et l'écart type de 1.
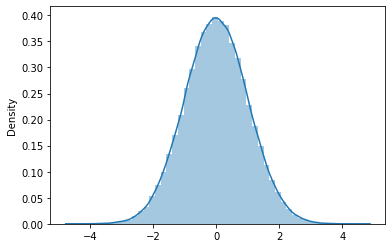
Il suit également la formule empirique selon laquelle le 68% des valeurs sont à 1 écart type de distance, les 95% pour cent d'entre eux sont 2 écarts types de distance et 99,7% sont à 3 écarts types par rapport à la moyenne. Cette propriété est très utile lors de la conception de tests d'hypothèses (https://www.statisticshowto.com/probability-and-statistics/hypothesis-testing/).
Le PDF est donné par,
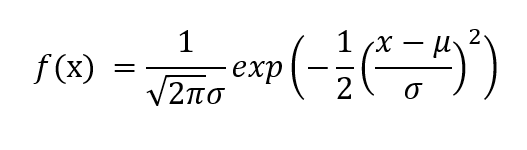
où est la moyenne de la variable aléatoire X et σ est l'écart type.
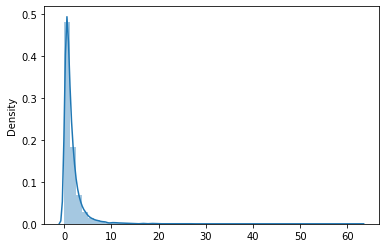
3. Distribution normale logarithmique
Cette distribution est utilisée pour représenter graphiquement les variables aléatoires dont les valeurs log suivent une distribution normale.. Considérez les variables aléatoires X et Y. Y = ln (X) est la variable qui est représentée dans cette distribution, où ln désigne le logarithme népérien des valeurs de X.
Le PDF est donné par,
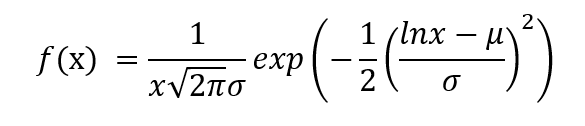
où est la moyenne de Y et σ est l'écart type de Y.
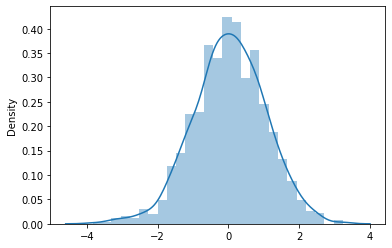
4. Distribution t de Student
La distribution t de Student est similaire à la distribution normale. La différence est que les queues de la distribution sont plus épaisses. Utilisé lorsque la taille de l'échantillon est petite et que la variance de la population est inconnue. Cette distribution est définie par les degrés de liberté (p) qui sont calculés comme la taille de l'échantillon moins 1 (m – 1).
Au fur et à mesure que la taille de l'échantillon augmente, augmentation des degrés de liberté, la distribution t se rapproche de la distribution normale et les queues deviennent plus étroites et la courbe se rapproche de la moyenne. Cette distribution est utilisée pour tester les estimations de la moyenne de la population lorsque la taille de l'échantillon est inférieure à 30 et la variance de la population est inconnue. Variance / l'écart type de l'échantillon est utilisé pour calculer la valeur t.
Le PDF est donné par,
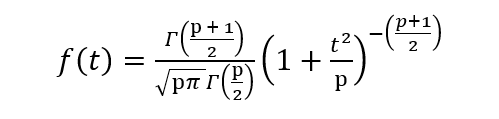
où p sont les degrés de liberté et est la fonction gamma. Voir ce lien pour une brève description de la fonction gamma.
La statistique t utilisée dans le test d'hypothèse est calculée comme suit,
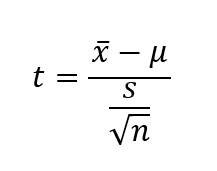
où x̄ est la moyenne de l'échantillon, μ est la moyenne de la population et s est la variance de l'échantillon.
5. Distribution du Khi deux
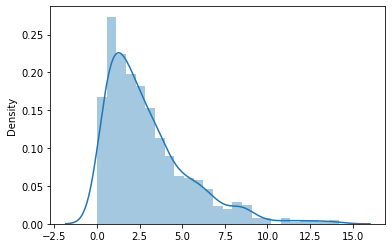
Cette distribution est égale à la somme des carrés de p variables aléatoires normales. p est le nombre de degrés de liberté. Comme la distribution t, à mesure que les degrés de liberté augmentent, la distribution se rapproche progressivement de la distribution normale. Ci-dessous, une distribution du chi carré avec trois degrés de liberté.
Le PDF est donné par,
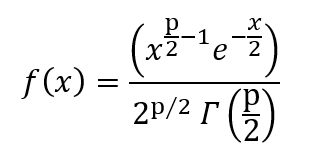
où p sont les degrés de liberté et est la fonction gamma.
La valeur du chi carré est calculée comme suit:
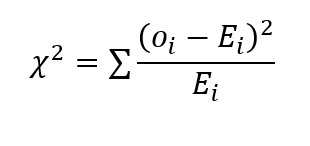
où o est la valeur observée et E représente la valeur attendue. Ceci est utilisé dans les tests d'hypothèses pour tirer des inférences sur la variance de la population des distributions normales..
6. Distribution exponentielle
Souvenez-vous de la distribution de probabilité discrète dont nous avons discuté dans l'article sur la probabilité discrète. Dans la distribution de Poisson, on prend l'exemple des appels reçus par le centre de service client. Dans cet exemple, nous considérons le nombre moyen d'appels par heure. À présent, dans cette répartition, le temps entre les appels successifs est expliqué.
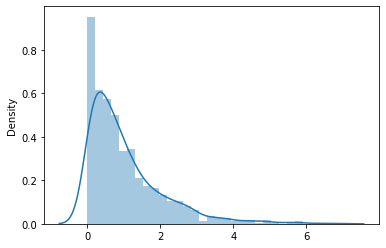
La distribution exponentielle peut être considérée comme l'inverse de la distribution de Poisson. Les événements considérés sont indépendants les uns des autres.
Le PDF est donné par,
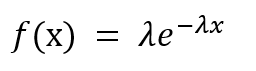
où est le paramètre de taux. = 1 / (temps moyen entre les événements).
Compléter, nous avons très brièvement discuté des différentes distributions de probabilités continues dans cet article. N'hésitez pas à ajouter des commentaires ou des suggestions ci-dessous.
Sur moi
Soja Priyanka Madiraju, un ancien ingénieur logiciel travaillant sur la transition vers la science des données. Je suis étudiant en Master Data Science. N'hésitez pas à me contacter sur https://www.linkedin.com/in/priyanka-madiraju
Les médias présentés dans cet article ne sont pas la propriété de DataPeaker et sont utilisés à la discrétion de l'auteur.
