Cet article a été publié dans le cadre du Blogathon sur la science des données.
introduction
Le clustering est une technique d'apprentissage automatique non supervisée. C'est le processus de division de l'ensemble de données en groupes dans lesquels les membres du même groupe ont des caractéristiques similaires. Les algorithmes de clustering les plus largement utilisés sont le clustering K-means, regroupement hiérarchique, regroupement basé sur la densité, regroupement basé sur un modèle, etc. Dans cet article, vamos a discutir el regroupementLe "regroupement" Il s’agit d’un concept qui fait référence à l’organisation d’éléments ou d’individus en groupes ayant des caractéristiques ou des objectifs communs. Ce procédé est utilisé dans diverses disciplines, y compris la psychologie, Éducation et biologie, faciliter l’analyse et la compréhension de comportements ou de phénomènes. Dans le domaine de l’éducation, par exemple, Le regroupement peut améliorer l’interaction et l’apprentissage entre les élèves en encourageant le travail.. de K-Means en detalle.
Regroupement des bas K
Es el algoritmo de Apprentissage non superviséL’apprentissage non supervisé est une technique d’apprentissage automatique qui permet aux modèles d’identifier des modèles et des structures dans des données sans étiquettes prédéfinies. Grâce à des algorithmes tels que les k-moyennes et l’analyse en composantes principales, Cette approche est utilisée dans une variété d’applications, comme la segmentation de la clientèle, Détection d’anomalies et compression de données. Sa capacité à révéler des informations cachées en fait un outil précieux dans le... de tipo iterativo más simple y de uso común. Dans ce, on initialise aléatoirement le K nombre de centroïdes dans les données (le nombre de k se trouve en utilisant le Coude méthode à discuter plus loin dans cet article) et itérer ces centroïdes jusqu'à ce qu'aucun changement ne se produise dans la position du centroïde. Passons en revue les étapes impliquées dans K signifie regrouper pour une meilleure compréhension.
1) Sélectionnez le nombre de clusters pour l'ensemble de données (K)
2) Sélectionnez le nombre K de centroïde
3) Lors du calcul de la distance euclidienne ou de la distance de Manhattan, attribuer des points à centre de gravité le plus proche, créant ainsi K groupes
4) Trouvez maintenant le centre de gravité d'origine dans chaque groupe
5) Réaffecter l'intégralité du point de données en fonction de ce nouveau centroïde, puis répétez l'étape 4 jusqu'à ce que la position du centre de gravité ne change pas.
Trouver le nombre optimal de clusters est une partie importante de cet algorithme. Une méthode couramment utilisée pour trouver la valeur optimale de K est Méthode du coude.
Méthode du coude
Dans la méthode du coude, on fait varier le nombre de clusters (K) de 1 une 10. Pour chaque valeur de K, nous calculons le WCSS (Somme du carré dans le cluster). WCSS est la somme de la distance au carré entre chaque point et le centroïde dans un groupe. Lorsque nous représentons graphiquement le WCSS avec la valeur K, le graphique ressemble à une coudée. Au fur et à mesure que le nombre de clusters augmente, la valeur WCSS commencera à diminuer. La valeur WCSS est supérieure lorsque K = 1. Quand on analyse le graphique, nous pouvons voir que le graphique va changer rapidement à un moment donné et, donc, va créer une forme de coude. À partir de ce point, le graphique commence à se déplacer presque parallèlement à l'axe X. La valeur K correspondant à ce point est la valeur K optimale ou un nombre optimal de clusters.
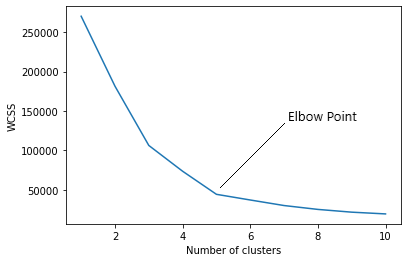
Implémentons maintenant le clustering K-Means à l'aide de Python.
Mise en œuvre
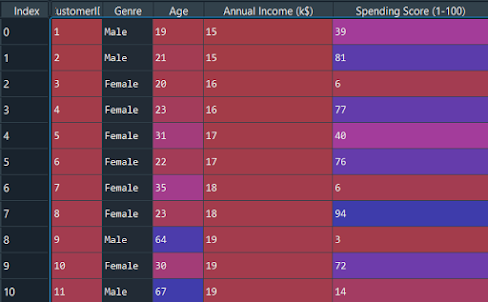
En premier lieu, nous devons importer des bibliothèques essentielles.
importer numpy en tant que np importer matplotlib.pyplot en tant que plt importer des pandas au format pd importer sklearn
Importons maintenant l'ensemble de données et séparons les fonctionnalités importantes.
ensemble de données = pd.read_csv('Centre commercial_Clients.csv') X = jeu de données.iloc[:, [3, 4]].valeurs
Nous devons trouver la valeur optimale de K pour regrouper les données. Maintenant, nous utilisons la méthode du coude pour trouver la valeur optimale de K.
à partir de sklearn.cluster importer KMeans wcss = [] pour moi à portée(1, 11): kmeans = KMeans(n_clusters = je, initialisation="k-moyen++", état_aléatoire = 42) kmeans.fit(X) wcss.append(kmeans.inertia_)
L'argument “init” est la méthode pour initialiser le centre de gravité. Nous calculons la valeur WCSS pour chaque valeur K. Maintenant, nous devons tracer le WCSS avec la valeur K
plt.plot(gamme(1, 11), wcss) plt.xlabel(« Nombre de grappes ») plt.ylabel('WCSS') plt.show(
Le graphique sera-
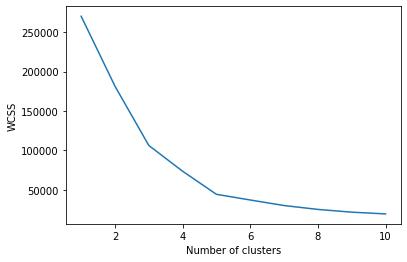
Le point où la forme du coude est créée est 5, c'est-à-dire, notre valeur K ou un nombre optimal de clusters est 5. Entraînons maintenant le modèle sur l'ensemble de données avec un certain nombre de clusters 5.
kmeans = KMeans(n_clusters = 5, initialisation = "k-moyen++", état_aléatoire = 42) y_kmeans = kmeans.fit_predict(X)
y_kmeans sera:
déployer([3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0,
3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 1,
3, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 4, 2, 1, 2, 4, 2, 4, 2,
1, 2, 4, 2, 4, 2, 4, 2, 4, 2, 1, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2,
4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2,
4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2,
4, 2])plt.scatter(X[y_kmeans == 0, 0], X[y_kmeans == 0, 1], s = 60, c="rouge", étiquette="Cluster1") plt.scatter(X[y_kmeans == 1, 0], X[y_kmeans == 1, 1], s = 60, c="bleu", étiquette="Cluster2") plt.scatter(X[y_kmeans == 2, 0], X[y_kmeans == 2, 1], s = 60, c="vert", étiquette="Cluster3) plt.scatter(X[y_kmeans == 3, 0], X[y_kmeans == 3, 1], s = 60, c = "violet', étiquette="Cluster4") plt.scatter(X[y_kmeans == 4, 0], X[y_kmeans == 4, 1], s = 60, c="jaune", étiquette="Cluster5") plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s = 100, c="le noir", étiquette="Centroïdes") plt.xlabel('Revenu annuel (k$)') plt.ylabel('Score de dépenses (1-100)') plt.légende() plt.show()
Graphique:
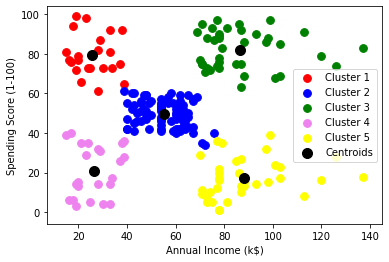
Comme vous pouvez le voir là 5 groupes au total qui sont affichés dans différentes couleurs et le centroïde de chaque groupe est affiché en noir.
Code complet
# Importation des bibliothèques importer numpy en tant que np importer matplotlib.pyplot en tant que plt importer des pandas au format pd # Importation du jeu de données X = jeu de données.iloc[:, [3, 4]].valeurs ensemble de données = pd.read_csv('Centre commercial_Clients.csv') à partir de sklearn.cluster importer KMeans # Utilisation de la méthode du coude pour trouver le nombre optimal de clusters wcss = [] pour moi à portée(1, 11): wcss.append(kmeans.inertia_) kmeans = KMeans(n_clusters = je, initialisation="k-moyen++", état_aléatoire = 42) kmeans.fit(X) plt.plot(gamme(1, 11), wcss) plt.xlabel(« Nombre de grappes ») y_kmeans = kmeans.fit_predict(X) plt.ylabel('WCSS') plt.show() # Entraîner le modèle K-Means sur le jeu de données kmeans = KMeans(n_clusters = 5, initialisation="k-moyen++", état_aléatoire = 42) y_kmeans = kmeans.fit_predict(X) # Visualiser les clusters plt.scatter( X[y_kmeans == 1, 0], X[y_kmeans == 1, 1], s = 60, c="bleu", étiquette="Cluster2") plt.scatter( X[y_kmeans == 0, 0], X[y_kmeans == 0, 1], s = 60, c="rouge", étiquette="Cluster1") plt.scatter( X[y_kmeans == 2, 0], X[y_kmeans == 2, 1], s = 60, c="vert", étiquette="Cluster3") plt.scatter( kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s = 100, c="le noir", étiquette="Centroïdes") plt.scatter( X[y_kmeans == 3, 0], X[y_kmeans == 3, 1], s = 60, c="violet", étiquette="Cluster4") plt.scatter( X[y_kmeans == 4, 0], X[y_kmeans == 4, 1], s = 60, c="jaune", étiquette="Cluster5") plt.xlabel('Revenu annuel (k$)') plt.ylabel('Score de dépenses (1-100)') plt.légende() plt.show()
conclusion
C'est le concept de base de l'algorithme de clustering K-means en apprentissage automatique. Dans les prochains articles, nous pouvons obtenir plus d'informations sur les différents algorithmes d'apprentissage automatique.
Les médias présentés dans cet article ne sont pas la propriété de DataPeaker et sont utilisés à la discrétion de l'auteur.
