Cet article a été publié dans le cadre du Blogathon sur la science des données.
Vue d'ensemble
Le clustering K-means est un algorithme d'apprentissage automatique non supervisé très célèbre et puissant. Utilisé pour résoudre de nombreux problèmes complexes d'apprentissage automatique non supervisé. Avant de commencer, Jetons un coup d'oeil aux points que nous allons comprendre.
Table des matières
- introduction
- Comment fonctionne l'algorithme K-means?
- Comment choisir la valeur de K?
- Méthode du coude.
- Méthode de la silhouette.
- Avantages des k-means.
- Inconvénients des k-means.
introduction
Entendamos el algoritmo de regroupementLe "regroupement" Il s’agit d’un concept qui fait référence à l’organisation d’éléments ou d’individus en groupes ayant des caractéristiques ou des objectifs communs. Ce procédé est utilisé dans diverses disciplines, y compris la psychologie, Éducation et biologie, faciliter l’analyse et la compréhension de comportements ou de phénomènes. Dans le domaine de l’éducation, par exemple, Le regroupement peut améliorer l’interaction et l’apprentissage entre les élèves en encourageant le travail.. de K-means con su definición simple.
Un algorithme de clustering K-means tente de regrouper des éléments similaires sous la forme de clusters. Le nombre de groupes est représenté par K.
Prenons un exemple. Supposons que vous alliez dans un magasin de légumes pour acheter des légumes. Vous y verrez différents types de légumes. La seule chose que vous remarquerez, c'est que les légumes seront rangés dans un groupe de leurs types. Comme toutes les carottes resteront au même endroit, les pommes de terre resteront avec leurs types et ainsi de suite. Si vous remarquez ici, alors vous constaterez qu'ils forment un groupe ou un groupe, où chacun des légumes est conservé dans son type de groupe formant les groupes.
Ahora entenderemos esto con la ayuda de una hermosa chiffre"Chiffre" est un terme utilisé dans divers contextes, De l’art à l’anatomie. Dans le domaine artistique, fait référence à la représentation de formes humaines ou animales dans des sculptures et des peintures. En anatomie, désigne la forme et la structure du corps. En outre, en mathématiques, "chiffre" Il est lié aux formes géométriques. Sa polyvalence en fait un concept fondamental dans de multiples disciplines.....
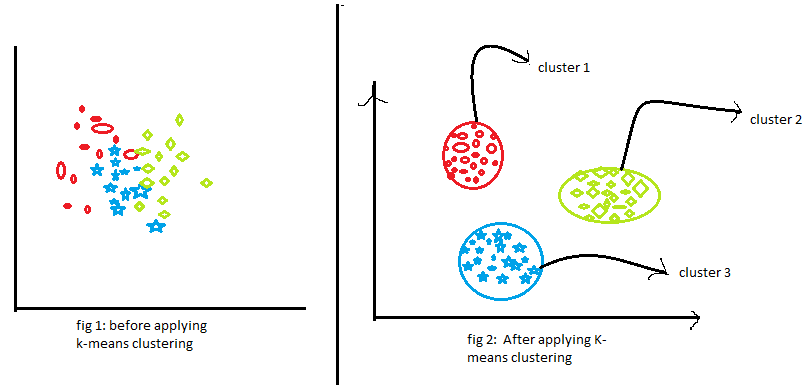
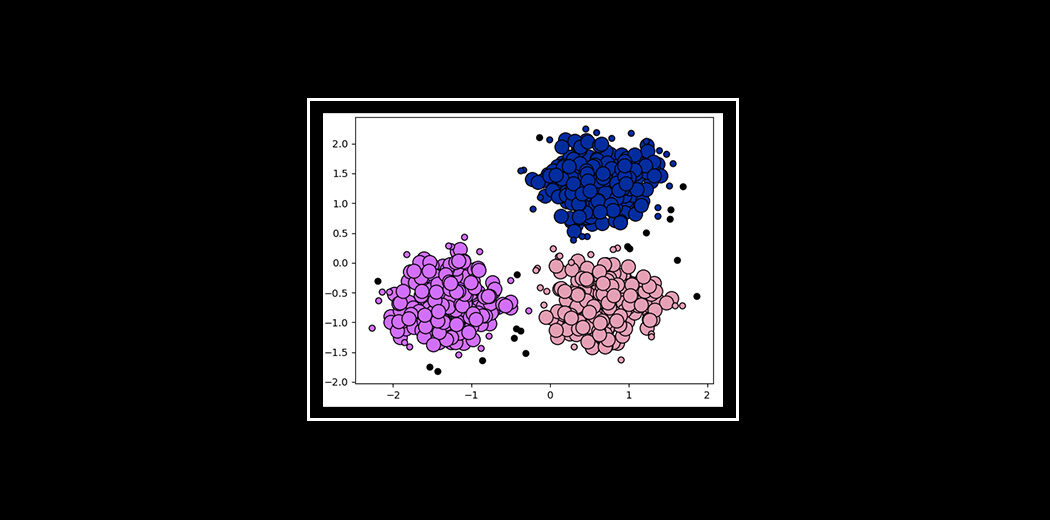
À présent, regardez les deux figures ci-dessus. Qu'avez-vous observé ? Parlons du premier chiffre. La première figure montre les données avant d'appliquer l'algorithme de clustering k-means. Ici, les trois catégories différentes sont en désordre. Quand vous voyez ces données dans le monde réel, vous ne pourrez pas connaître les différentes catégories.
À présent, regarde le deuxième chiffre (chiffre 2). Cela montre les données après l'application de l'algorithme de clustering K-means. vous pouvez voir que les trois éléments différents sont classés en trois catégories différentes appelées groupes.
Comment fonctionne l'algorithme de clustering K-means?
Le regroupement K-means tente de regrouper des types d'éléments similaires sous forme de regroupements. Trouver la similitude entre les éléments et les regrouper en groupes. L'algorithme de clustering K-means fonctionne en trois étapes. Voyons quelles sont ces trois étapes.
- Sélectionnez les valeurs k.
- Initialiser les centroïdes.
- Sélectionnez le groupe et trouvez la moyenne.
Comprenons les étapes ci-dessus à l'aide de la figure car une bonne image vaut mieux que des milliers de mots.
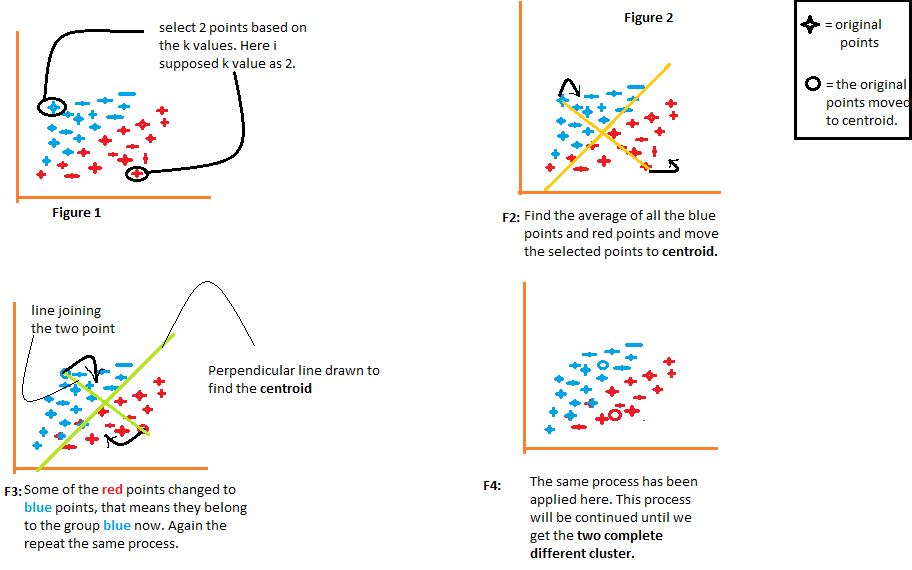
Nous allons comprendre chaque chiffre un par un.
- La figure 1 montre la représentation des données de deux éléments différents. le premier élément est affiché en bleu et le deuxième élément est affiché en rouge. Ici, je choisis la valeur de K au hasard comme 2. Il existe différentes méthodes par lesquelles nous pouvons choisir les bonnes valeurs k.
- Dans la figure 2, joindre les deux points sélectionnés. À présent, pour trouver le centre de gravité, nous allons tracer une ligne perpendiculaire à cette ligne. Les points se déplaceront vers leur centroïde. Si tu regardes là, vous verrez que certains des points rouges se déplacent maintenant vers les points bleus. À présent, ces points appartiennent au groupe des éléments bleus.
- Le même processus se poursuivra dans la figure 3. Nous allons joindre les deux points et nous allons tracer une ligne perpendiculaire à cela et nous allons trouver le centre de gravité. Maintenant, les deux points se déplaceront vers leur centre de gravité et à nouveau certains des points rouges se transformeront en points bleus.
- Le même processus se produit dans la figure 4. Ce processus se poursuivra jusqu'à ce que nous obtenions deux groupes complètement différents de ces groupes.
REMARQUE: Notez que le regroupement des K-moyennes utilise la méthode de la distance euclidienne pour connaître la distance entre les points.
Vous trouverez de nombreuses explications sur la distance euclidienne sur Internet.
Comment choisir la valeur de K?
L'une des tâches les plus difficiles de cet algorithme de clustering est de choisir les valeurs correctes de k. Quelle devrait être la valeur k correcte? Comment choisir la valeur k? Trouvons la réponse à ces questions. Si vous choisissez les k valeurs au hasard, ça peut être bien ou mal. Si vous choisissez la mauvaise valeur, affectera directement les performances de votre modèle. Ensuite, Il existe deux méthodes par lesquelles vous pouvez sélectionner la valeur correcte de k.
- Méthode du coude.
- Méthode de la silhouette.
À présent, comprenons les deux concepts un par un en détail.
Méthode du coude
Le coude est l'une des méthodes les plus connues par laquelle vous pouvez sélectionner la valeur correcte de k et augmenter les performances de votre modèle. Nous effectuons également un réglage des hyperparamètres pour choisir la meilleure valeur de k. Voyons comment fonctionne cette méthode du coude.
C'est une méthode empirique pour trouver la meilleure valeur de k. recueillir l'éventail des valeurs et en tirer le meilleur. Calculer la somme du carré des points et calculer la distance moyenne.
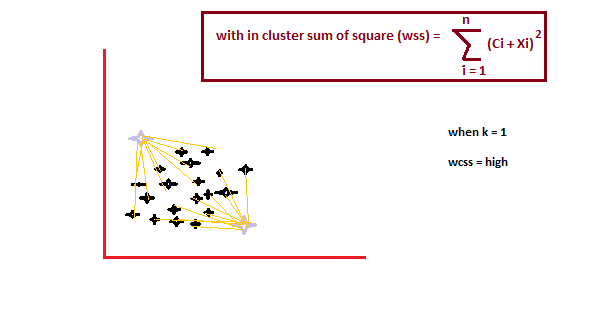
Lorsque la valeur de k est 1, la somme du carré au sein du groupe sera élevée. UNE mesureLa "mesure" C’est un concept fondamental dans diverses disciplines, qui fait référence au processus de quantification des caractéristiques ou des grandeurs d’objets, phénomènes ou situations. En mathématiques, Utilisé pour déterminer les longueurs, Surfaces et volumes, tandis qu’en sciences sociales, il peut faire référence à l’évaluation de variables qualitatives et quantitatives. La précision des mesures est cruciale pour obtenir des résultats fiables et valides dans toute recherche ou application pratique.... que aumenta el valor de k, la somme de la valeur au carré au sein du groupe diminuera.
Finalement, nous allons tracer un graphique entre les k valeurs et la somme du carré au sein du groupe pour obtenir la k valeur. Nous examinerons attentivement le graphique. Dans quelque moment, notre graphique va diminuer brutalement. Ce point sera considéré comme une valeur de k.
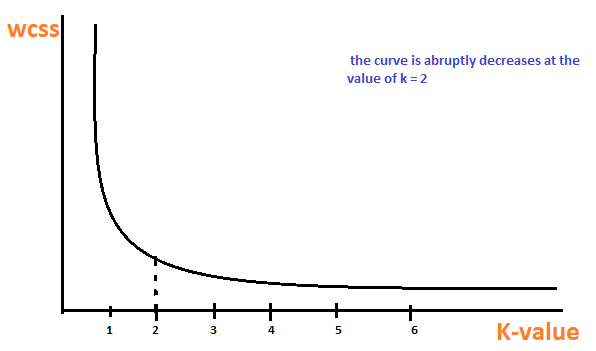
Méthode de la silhouette
La méthode de la silhouette est quelque peu différente. La méthode du coude prend également la plage de valeurs k et dessine le graphique de la silhouette. Calculer le coefficient de silhouette de chaque point. Trouvez la distance moyenne des points au sein de votre groupe à (je) et la distance moyenne des points à leur prochain groupe le plus proche appelé b (je).

Noter: La A (je) la valeur doit être inférieure à b (je) valeur, qu'est-ce que l'IA << avec un.
À présent, nous avons les valeurs d'un (je) et B (je). nous allons calculer le coefficient de silhouette en utilisant la formule suivante.
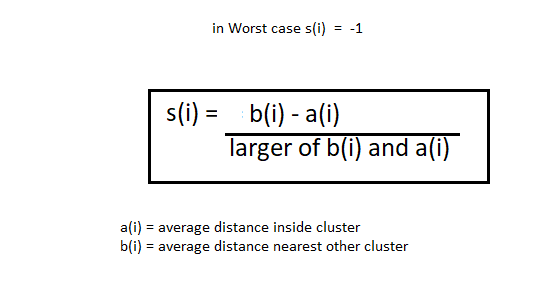
À présent, nous pouvons calculer le coefficient de silhouette de tous les points dans les groupes et tracer le graphique de la silhouette. Ce graphique sera également utile pour détecter les valeurs aberrantes. L'intrigue de la silhouette est entre -1 une 1.
A noter que pour le coefficient de silhouette égal à -1 est le pire des cas.
Regardez le graphique et vérifiez laquelle des valeurs k est la plus proche de 1.
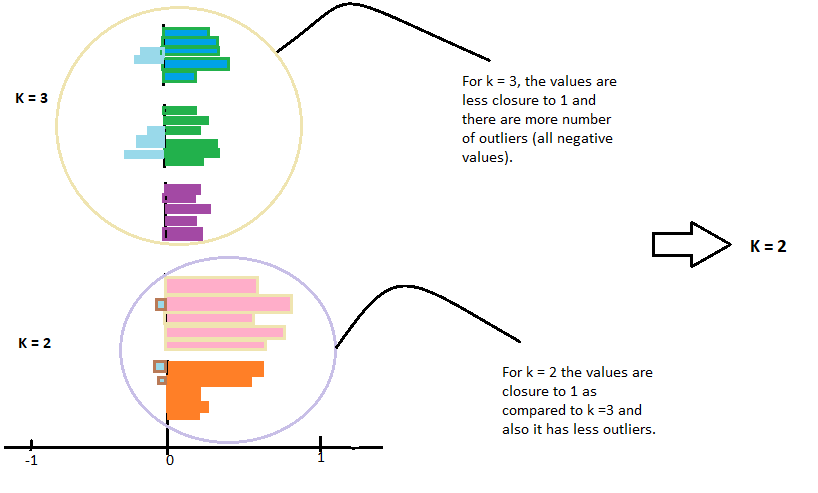
En outre, vérifier le graphique qui a le moins de valeurs aberrantes, ce que signifie une valeur moins négative. Ensuite, choisissez cette valeur de k pour votre modèle pour l'ajuster.
Avantages des K-means
- C'est très simple à mettre en oeuvre.
- Il est évolutif pour un grand ensemble de données et également plus rapide pour de grands ensembles de données.
- adapter de nouveaux exemples très souvent.
- Généralisation des clusters pour différentes formes et tailles.
Inconvénients des K-means
- Il est sensible aux valeurs aberrantes.
- Choisir manuellement les valeurs k est un travail difficile.
- Au fur et à mesure que le nombre de dimensions augmente, son évolutivité diminue.