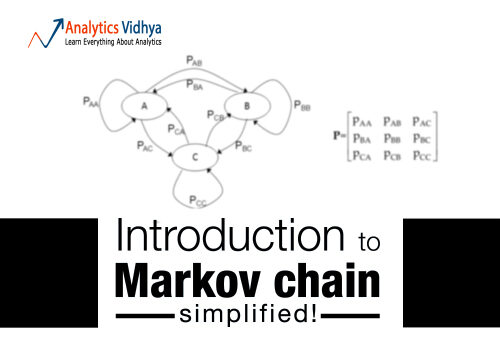
A cadeia de Markov é um conceito simples que pode explicar os processos em tempo real mais complicados. Reconhecimento de voz, identificadores de texto, reconhecimento de caminho e muitas outras ferramentas de inteligência artificial usam este princípio simples chamado de cadeia de Markov de alguma forma. Neste artigo, ilustraremos como esse conceito é fácil de entender e implementá-lo no R.
A cadeia de Markov é baseada no princípio de “perda de memória”. Em outras palavras, o próximo estado do processo depende apenas do estado anterior e não da sequência de estados. Essa suposição simples facilita o cálculo da probabilidade condicional e permite que esse algoritmo seja aplicado em vários cenários.. Neste artigo, nos limitaremos a uma simples cadeia de Markov. Em problemas da vida real, geralmente usamos o modelo de Markov latente, que é uma versão altamente evoluída da cadeia de Markov. Também falaremos sobre uma aplicação simples da cadeia de Markov no próximo artigo..
Um caso de negócios simples
Coca-Cola e Pepsi são as únicas empresas do país X. Uma empresa de refrigerantes deseja se associar a um desses concorrentes. Eles contratam uma empresa de pesquisa de mercado para descobrir qual das marcas terá uma maior participação de mercado após 1 minha. Atualmente, Pepsi possui o 55% e a Coca é dona da 45% de participação de mercado. Abaixo estão as conclusões tiradas pela empresa de pesquisa de mercado:
P (P-> P): Probabilidade de um cliente ficar com a marca Pepsi por um mês = 0,7
P (P-> C): probabilidade de um cliente mudar de Pepsi para Coca-Cola em um mês = 0,3
P (C-> C): Probabilidade de um cliente ficar com a marca Coca por um mês = 0.9
P (C-> P): Probabilidade de que um cliente mude da Coca-Cola para a Pepsi em um mês = 0,1
Podemos ver claramente que os clientes tendem a ficar com a Coca-Cola, mas a Coca-Cola atualmente tem uma participação menor na carteira. Portanto, não podemos ter certeza da recomendação sem fazer alguns cálculos de transição.
Diagrama de transição
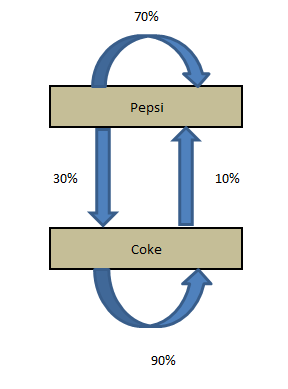
As quatro declarações feitas pela empresa de pesquisa podem ser estruturadas em um diagrama de transição simples.
O diagrama simplesmente mostra as transições e a participação de mercado atual. Agora, se quisermos calcular a participação de mercado após um mês, devemos fazer os seguintes cálculos:
Cota de mercado (t + 1) Pepsi = a participação de mercado atual da Pepsi * P (P-> P) + A participação de mercado atual da Coca-Cola * P (C-> P)
Quota de mercado (t + 1) Coca-Cola = participação de mercado atual da Coca-Cola * P (C-> C) + A participação de mercado atual da Pepsi * P (P-> C)
Esses cálculos podem ser feitos simplesmente observando a seguinte multiplicação de matrizes:
Matriz de transição do estado atual X = estado final
Como podemos ver, vemos claramente que a Pepsi, embora tenha uma maior participação de mercado agora, terá uma participação de mercado menor após um mês. Este cálculo simples é chamado de cadeia de Markov.. Se a matriz de transição não mudar ao longo do tempo, podemos prever a participação de mercado em qualquer momento futuro. Vamos fazer o mesmo cálculo para 2 meses depois.
Cálculos de estado estacionário
Além do caso de negócios que nos preocupa, a empresa de refrigerantes quer reduzir a lacuna de participação de mercado da empresa Coca e Pepsi no longo prazo. Isso os ajudará a definir a estratégia de custo certa ao mergulhar na Coca-Cola.. A participação da Pepsi continuará diminuindo a um ponto em que o número de clientes deixando a Pepsi e o número de clientes que se adaptam à Pepsi é o mesmo. Portanto, precisamos satisfazer as seguintes condições para encontrar as proporções de estado estacionário:
Pepsi MS * 30% = Coca-Cola MS * 10% …………………………………………… ..1
Pepsi MS + Coca-Cola MS = 100% …………………………………………………… 2
4 * Pepsi MS = 100% => Pepsi MS = 25% e Coca-Cola MS = 75%
Vamos formular um algoritmo para encontrar o estado estacionário. Depois de estado estacionário, multiplicar o estado inicial pela matriz de transição dará o próprio estado inicial. Por tanto, a matriz que pode satisfazer a seguinte condição serão as proporções finais:
Estado inicial X Matriz de transição = estado inicial
Resolvendo a equação acima, podemos encontrar a matriz de estado estacionário. A solução será a mesma que [25%,75%].
Agora vamos resolver o exemplo anterior em R.
Implementação em R
Paso 1: criando uma matriz de transição e uma cadeia de Markov de tempo discreto
Produção
trans_mat [,1] [,2] [1,] 0.7 0.3 [2,] 0.1 0.9 #create the Discrete Time Markov Chain MC 1 UMA 2 - cadeia de markov discreta dimensional definida pelos seguintes estados: Pepsi, Coke The transition matrix (por linhas) é definido como segue: Pepsi Coke Pepsi 0.7 0.3 Coque 0.1 0.9
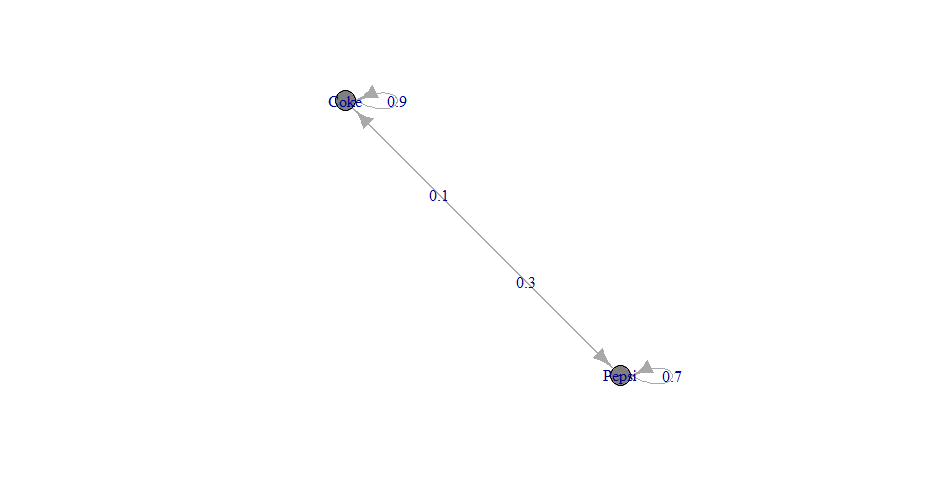
Enredo
Paso 2: Calcular a participação de mercado após 1 mês e 2 meses
Produção
#Market Share after one month Pepsi Coke 0.43 0.57 #Market Share after two month Pepsi Coke 0.358 0.642
Paso 3: criando uma matriz de estado estável
Produção
Pepsi Coca-Cola 0.25 0.75
Notas finais
Neste artigo, apresentamos as equações da cadeia de Markov, terminologia e sua implementação em R. Também discutimos como equações simples podem ser escaladas usando a multiplicação de matrizes.. Usaremos essas terminologias e estrutura para resolver um exemplo da vida real no próximo artigo.. También le presentaremos conceptos como nóO Nodo é uma plataforma digital que facilita a conexão entre profissionais e empresas em busca de talentos. Através de um sistema intuitivo, permite que os usuários criem perfis, Compartilhar experiências e acessar oportunidades de trabalho. Seu foco em colaboração e networking torna o Nodo uma ferramenta valiosa para quem deseja expandir sua rede profissional e encontrar projetos que se alinhem com suas habilidades e objetivos.... absorvente y cadena de Markov regular para resolver el ejemplo.
O artigo foi útil para você? Este artigo resolveu algum dos seus problemas existentes? Você já usou uma cadeia de Markov simples antes? Se você fez, compartilhe conosco seus pensamentos sobre o assunto.