Função de custo | Tipos de aprendizado de máquina de função de custo

Este artigo foi publicado como parte do Data Science Blogathon.

Crédito: https://gifer.com/en/GxlE

As 2 As principais questões que surgiram em minha mente enquanto trabalhava neste artigo foram “Por que estou escrevendo este artigo?” & “Como meu artigo difere de outros artigos?” Nós vamos, a função de custo é um conceito importante para entender nos campos da ciência de dados, mas enquanto eu estava seguindo minha graduação, Percebi que os recursos disponíveis online são muito gerais e não cobrem completamente minhas necessidades.

Tive que consultar muitos artigos e assistir alguns vídeos no YouTube para ter uma ideia das funções de custo. Como resultado, Eu queria reunir as funções “Este”, “Quando”, “Quão” e “Por que” de Custo que pode ajudar a explicar este tópico de forma mais clara. Espero que meu artigo funcione como um balcão único para funções de custo!!

Guia fictício para função de custo 🤷‍♀️

Função de perdaA função de perda é uma ferramenta fundamental no aprendizado de máquina que quantifica a discrepância entre as previsões do modelo e os valores reais. Seu objetivo é orientar o processo de treinamento, minimizando essa diferença, permitindo assim que o modelo aprenda de forma mais eficaz. Existem diferentes tipos de funções de perda, como erro quadrático médio e entropia cruzada, cada um adequado para diferentes tarefas e...: se utiliza cuando nos referimos al error de un solo ejemplo de TreinamentoO treinamento é um processo sistemático projetado para melhorar as habilidades, Conhecimento ou habilidades físicas. É aplicado em várias áreas, como esporte, Educação e desenvolvimento profissional. Um programa de treinamento eficaz inclui planejamento de metas, prática regular e avaliação do progresso. A adaptação às necessidades individuais e a motivação são fatores-chave para alcançar resultados bem-sucedidos e sustentáveis em qualquer disciplina.....
Função de custo: é usado para fazer referência a uma média das funções de perda em um conjunto de dados de treinamento completo.

Mas, * Porque * use uma função de custo?

Por que diabos precisamos de uma função de custo? Considere um cenário no qual queremos classificar os dados. Suponha que temos os detalhes de altura e peso de alguns cães e gatos. Vamos usar estes 2 características para classificá-los corretamente. Se rastrearmos esses registros, obtenemos el siguiente Diagrama de dispersãoO gráfico de dispersão é uma ferramenta gráfica usada em estatística para visualizar a relação entre duas variáveis. Consiste em um conjunto de pontos em um plano cartesiano, onde cada ponto representa um par de valores correspondentes às variáveis analisadas. Este tipo de gráfico permite identificar padrões, Tendências e possíveis correlações, facilitando a interpretação dos dados e a tomada de decisão com base nas informações visuais apresentadas....:

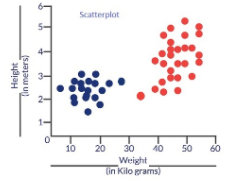
FIG 1: Gráfico de dispersão para altura e peso de vários cães e gatos

Os pontos azuis são gatos e os pontos vermelhos são cachorros. Abaixo estão algumas soluções para o problema de classificação acima.

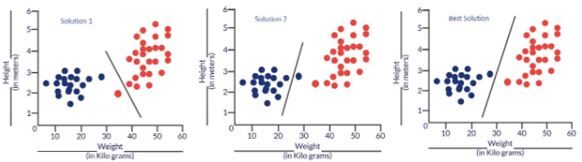
FIG: Soluções prováveis ​​para nosso problema de classificação

Essencialmente, todos os três classificadores têm uma precisão muito alta, mas a terceira solução é a melhor porque não classifica mal nenhum ponto. A razão pela qual classifica todos os pontos perfeitamente é que a linha está quase exatamente entre os dois grupos e não está mais próxima de nenhum deles.. É aqui que entra o conceito de função de custo.. A função de custo nos ajuda a chegar à solução ideal. A função de custo é a técnica de avaliação “o desempenho do nosso algoritmo / modelo”.

Obtém os resultados esperados pelo modelo e os resultados reais, e calcular o quão errado o modelo estava em sua previsão. Produz um número maior se nossas previsões diferem muito dos valores reais. UMA mediro "medir" É um conceito fundamental em várias disciplinas, que se refere ao processo de quantificação de características ou magnitudes de objetos, Fenômenos ou situações. Na matemática, Usado para determinar comprimentos, Áreas e volumes, enquanto nas ciências sociais pode se referir à avaliação de variáveis qualitativas e quantitativas. A precisão da medição é crucial para obter resultados confiáveis e válidos em qualquer pesquisa ou aplicação prática.... que ajustamos nuestro modelo para mejorar las predicciones, a função de custo atua como um indicador de como o modelo melhorou. Este é essencialmente um problema de otimização. As estratégias de otimização sempre visam "minimizar a função de custo".

Tipos de funções de custo

Existem muitas funções de custo no aprendizado de máquina e cada uma tem seus casos de uso, dependendo se é um problema de regressão ou classificação..

1. Função de custo de regressão
2. Funções de custo de classificação binária
3. Funções de custo de classificação de múltiplas classes

1. Função de custo de regressão:

Modelos de regressão tentam prever um valor contínuo, por exemplo, o salário de um empregado, o preço de um carro, prevendo um empréstimo, etc. Uma função de custo usada no problema de regressão é chamada “Função de custo de regressão”. Eles são calculados no erro com base na distância da seguinte forma:

Erro = y-y ‘

Onde,

E – Entrada real

E '- Partida planejada

As funções de custo de regressão mais comumente usadas estão abaixo,

1.1 Erro médio (MIM)

• Nesta função de custo, o erro é calculado para cada dado de treinamento e, em seguida, o valor médio de todos esses erros é derivado.
• Calcular a média dos erros é a forma mais simples e intuitiva possível.
• Os erros podem ser negativos e positivos. Portanto, podem cancelar um ao outro durante a soma, o que dá um erro médio zero para o modelo.
• Portanto, esta não é uma função de custo recomendada, mas estabelece a base para outras funções de custo de modelos de regressão.

1.2 Raiz do erro quadrático médio (MSE)

• Isso melhora a desvantagem que encontramos no erro acima da média. Aqui, um quadrado da diferença entre o valor real e previsto é calculado para evitar qualquer possibilidade de erro negativo.
• É medido como a média da soma das diferenças quadradas entre as previsões e as observações reais.

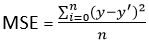
MSE = (soma dos erros quadrados) / n

• Também conhecido como perda L2.
• Em MSE, uma vez que cada erro é elevado ao quadrado, ajuda a penalizar mesmo pequenos desvios na previsão em comparação com MAE. Mas se nosso conjunto de dados tem outliers que contribuem para erros de previsão maiores, então, quadrar este erro ainda mais aumentará o erro muitas vezes mais e também levará a um erro MSE maior.
• Portanto, podemos dizer que é menos robusto para outliers.

1.3 Erro médio absoluto (MUITO DE)

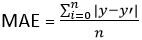
ISSO = (soma dos erros absolutos) / n

2. Funções de custo para problemas de classificação

As funções de custo usadas nos problemas de classificação são diferentes daquelas usadas no problema de regressão.. Uma função de perda comumente usada para classificação é a perda de entropia cruzada. Vamos entender a entropia cruzada com um pequeno exemplo. Considere que temos um problema de classificação de 3 classes como segue.

Classe (laranja, maçã, tomate)

O modelo de aprendizado de máquina dará uma distribuição de probabilidade desses 3 classes como saída para um dado dado de entrada. A classe com a maior probabilidade é considerada uma classe vencedora para a previsão.

Saída = [P(laranja),P(maçã),P(Tomate)]

A distribuição de probabilidade real para cada classe é mostrada abaixo.

Laranja = [1,0,0]

Apple = [0,1,0]

Tomate = [0,0,1]

Se durante a fase de treinamento, a classe de entrada é tomate, a distribuição de probabilidade prevista deve tender para a distribuição de probabilidade real do Tomate. Se a distribuição de probabilidade prevista não for mais próxima da real, o modelo deve ajustar seu peso. É aqui que a entropia cruzada se torna uma ferramenta para calcular a distância entre a distribuição de probabilidade prevista e a real.. Em outras palavras, entropia cruzada pode ser pensada como uma forma de medir a distância entre duas distribuições de probabilidade. A imagem a seguir ilustra a intuição por trás da entropia cruzada:

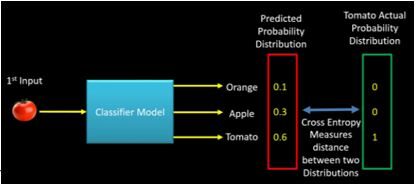
FIGURA"Figura" é um termo usado em vários contextos, Da arte à anatomia. No campo artístico, refere-se à representação de formas humanas ou animais em esculturas e pinturas. Em anatomia, designa a forma e a estrutura do corpo. O que mais, em matemática, "figura" está relacionado a formas geométricas. Sua versatilidade o torna um conceito fundamental em várias disciplinas.... 3: Intuição por trás da croosentropia (crédito – machinelearningknowledge.ai)

Esta foi apenas uma intuição por trás da entropia cruzada. Tem sua origem na teoria da informação. Agora, com este entendimento de entropia cruzada, vamos agora olhar para as funções de custo de classificação.

2.1 Funções de custo de classificação de múltiplas classes

Esta função de custo é usada em problemas de classificação onde existem várias classes e os dados de entrada pertencem a uma única classe. Vamos agora entender como a entropia cruzada é calculada. Suponha que o modelo forneça a distribuição de probabilidade conforme mostrado abaixo para 'n’ classes e para um dado de entrada particular D.

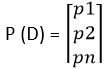
E a distribuição de probabilidade real ou alvo dos dados D é

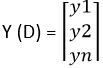
Mais tarde, a entropia cruzada para esse dado particular D é calculada como

Perda de entropia cruzada (e, p) = – e^T Cadastro (p)

= – (e₁ registro (p₁) + e₂ registro (p₂) + …… e_Norte registro (p_Norte))

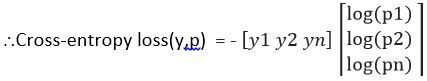
Vamos agora definir a função de custo usando o exemplo anterior (Veja a imagem de entropia cruzada -Fig3),

p (tomate) = [0.1, 0.3, 0.6]

e (tomate) = [0, 0, 1]

Entropia cruzada (D) = – e * registro (p) quando y = 1

Entropia cruzada (D) = – (1-e) * registro (1-p) quando y = 0

Entropia cruzada binária = (Soma de entropia cruzada para dados N) / N

conclusão

Relacionado