Otimização de portfólio em Python | Teoria de portfólio moderna em Python

Introdução

Neste artigo, Vamos aprender os conceitos de gerenciamento de portfólio e implementá-los usando bibliotecas Python.

O artigo é dividido em três partes, a fim de cobrir os fundamentos da gestão de portfólio, conforme mostrado abaixo:

1. Retorno sobre um ativo e um portfólio

2. Risco associado a um ativo e um portfólio

3. Teoria de portfólio moderna: encontre o portfólio ideal

Retorno sobre um ativo e um portfólio

Antes de mergulharmos no cálculo do retorno de um ativo e um portfólio, vamos visitar brevemente a definição de portfólio e retornos.

pasta: Uma carteira é uma coleção de instrumentos financeiros, como ações, títulos, matérias primas, Caixa e equivalentes de caixa, bem como suas contrapartes de fundos. [Investopedia]

Neste artigo, teremos nosso portfólio que contém 4 ativos (“Portfólio com foco em ações“): Ações da Apple Inc., Nike (NKC), Google e Amazon. A visualização de nossos dados é mostrada abaixo:

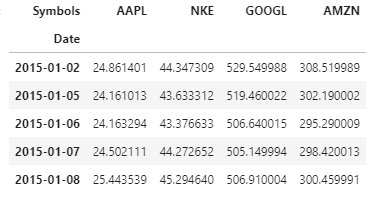
Devoluções: Refere-se ao ganho ou perda de nossos ativos / portfólio por um período fixo de tempo. Nesta análise, fazemos um retorno como a variação percentual no preço de fechamento do ativo em relação ao preço de fechamento do dia anterior. Vamos calcular os retornos usando.pct_change () função em python.

Abaixo está o código Python para fazer o mesmo e o 5 filas superiores (cabeçalho) de retornos

Observação: a primeira linha é nula se não houver linha anterior para facilitar o cálculo da mudança percentual.

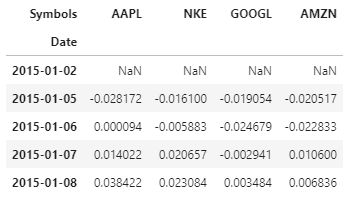
Devolver uma carteira é definido como a soma ponderada dos retornos sobre os ativos do portfólio.

Para demonstrar como calcular o desempenho do portfólio em Python, vamos inicializar os pesos aleatoriamente (que iremos otimizar). O retorno do portfólio é calculado conforme mostrado no código abaixo e o cabeçalho dos retornos do portfólio também é exibido:

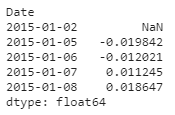
Vimos como calcular retornos, agora vamos mudar nosso foco para outro conceito: Risco

O risco associado a ativos e portfólio

O método para calcular o risco de uma carteira está escrito abaixo e posteriormente explicamos e damos a formulação matemática para cada uma das etapas:

• Calcule a matriz de covariância nos dados de desempenho.
• Anualize a covariância multiplicando por 252
• Calcule a variância da carteira, multiplicando-a pelos vetores de peso.
• Calcule a raiz quadrada da variância calculada acima para obter o desvio padrão. Este desvio padrão é chamado de volatilidade da carteira.

A fórmula para calcular a covariância e anualizá-la é:

covariance = returns.cov () * 252

como está lá 252 dias úteis, nós multiplicamos a covariância por 252 para anualizar.

A variação da carteira, a ser calculado na etapa 3 anterior, depende dos pesos dos ativos na carteira e é definido como:

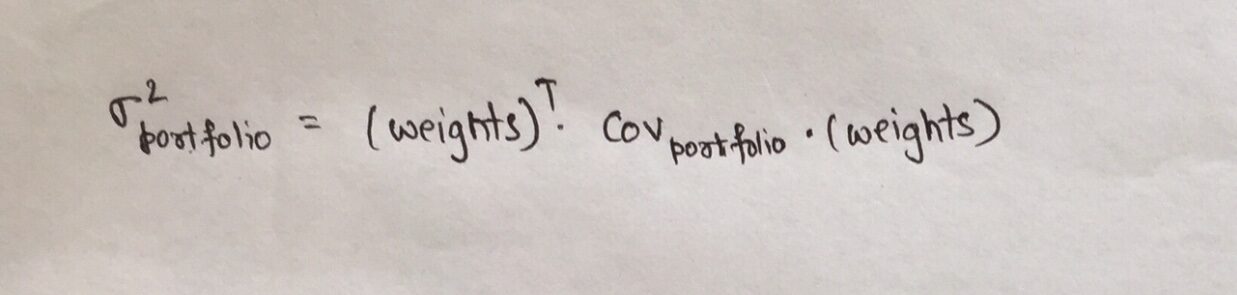
Onde,

• o_pasta é a matriz de covariância do portfólio
• pesos é o vetor de pesos atribuídos a cada ativo no portfólio

Abaixo está a abordagem para calcular o risco de ativos em Python.

Como explicado acima, nós multiplicamos a matriz de covariância com 252, como não 252 dias de negociação em um ano.

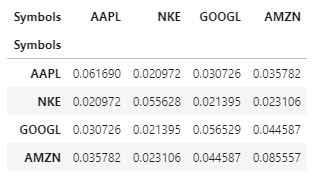
Os elementos diagonais de varnce_matrix representam a variação de cada ativo, enquanto os termos fora da diagonal representam a covariância entre os dois ativos, por exemplo: o elemento (1,2) representa a covariância entre Nike e Apple.

O código para calcular o risco do portfólio em python, cujo método vimos antes, é como mostrado:

Agora, a tarefa para nós é otimizar os pesos. Por que? Para que possamos maximizar nosso retorno ou minimizar nosso risco, E fazemos isso usando a teoria de portfólio moderna!!

Teoria de portfólio moderna

A teoria de portfólio moderna sustenta que as características de risco e retorno de um investimento não devem ser consideradas isoladamente, Em vez disso, eles devem ser avaliados com base em como o investimento afeta o risco geral e o retorno da carteira.. O MPT mostra que um investidor pode construir uma carteira de vários ativos que maximizará os retornos para um determinado nível de risco.. além do que, além do mais, dado um nível desejado de retorno esperado, um investidor pode construir uma carteira com o menor risco possível. Com base em medidas estatísticas, como variância e correlação, o desempenho de um investidor individual é menos importante do que como afeta todo o portfólio. [Investopedia]

Esta teoría se resume en la siguiente figura"Figura" é um termo usado em vários contextos, Da arte à anatomia. No campo artístico, refere-se à representação de formas humanas ou animais em esculturas e pinturas. Em anatomia, designa a forma e a estrutura do corpo. O que mais, em matemática, "figura" está relacionado a formas geométricas. Sua versatilidade o torna um conceito fundamental em várias disciplinas..... Encontramos a fronteira conforme mostrado abaixo e maximizamos o retorno esperado para o nível de risco ou minimizamos o risco para um determinado nível de retorno esperado.

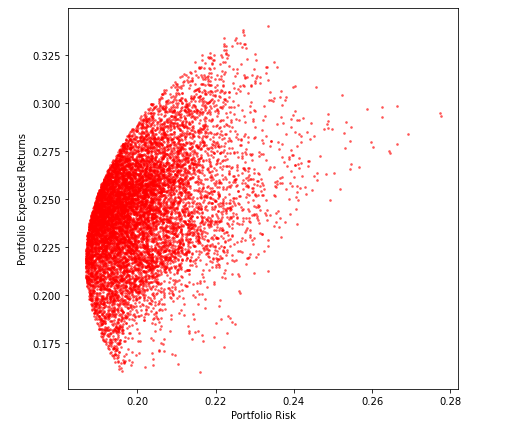
Nosso objetivo é escolher os pesos de cada ativo em nosso portfólio de forma que maximizemos o retorno esperado dado um nível de risco..

Matematicamente, a função objetivo pode ser definida como mostrado abaixo:

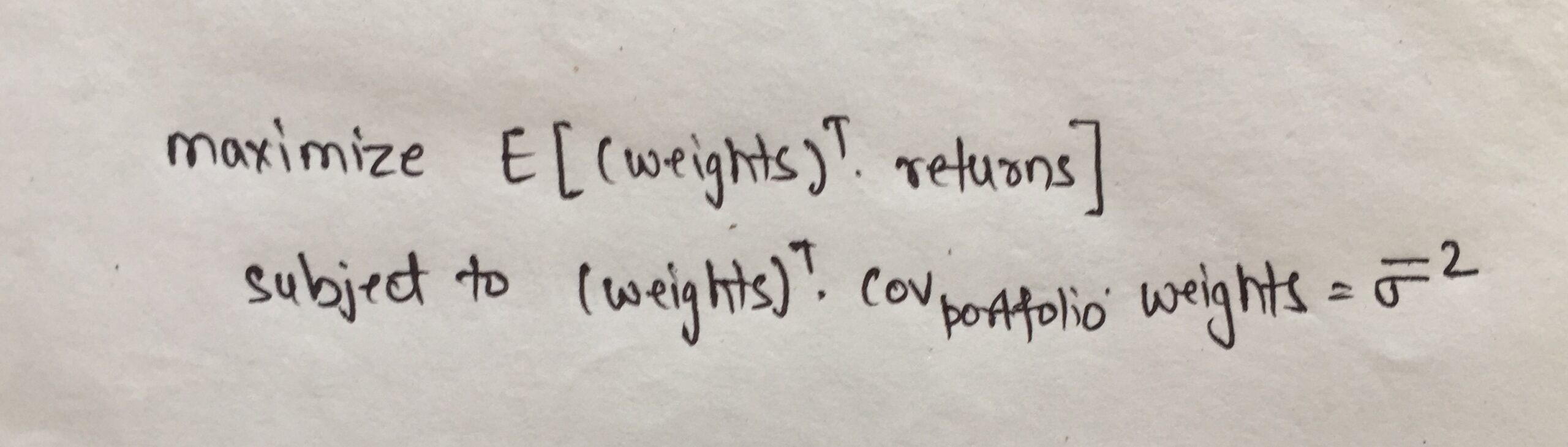
Outra forma de olhar para a Fronteira Eficiente e a função objetivo é que podemos minimizar o risco dado que o retorno esperado é pelo menos maior do que o valor dado.. Matematicamente, esta função objetivo pode ser escrita como:

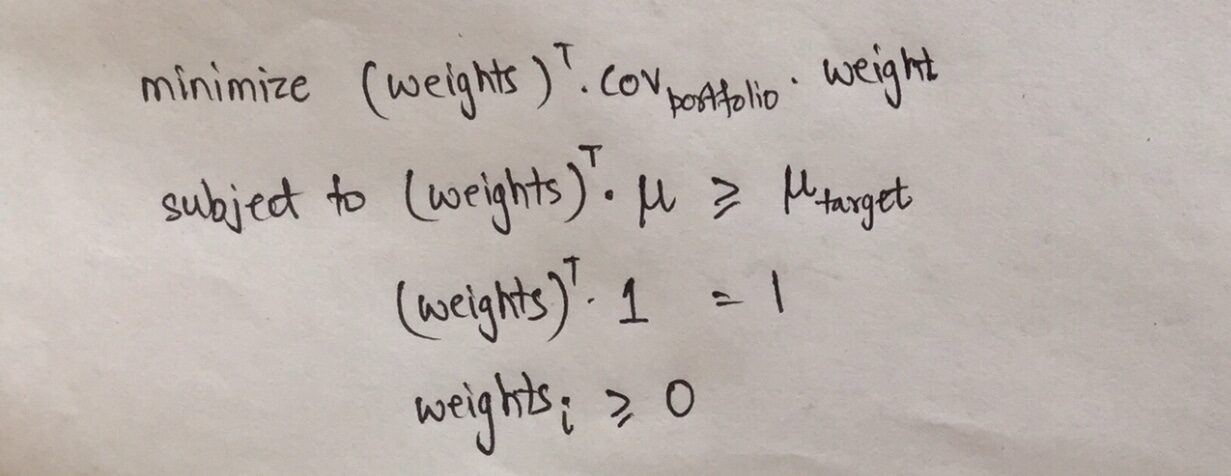
a primeira linha representa que o objetivo é minimizar a variância do portfólio, quer dizer, por sua vez, a volatilidade da carteira e, por tanto, minimizar o risco.

Restrito implica que os retornos devem ser maiores do que um retorno alvo específico, todos os pesos devem adicionar 1 e os pesos não devem ser negativos.

Agora que conhecemos o conceito, Vamos passar para a parte prática agora!

Em primeiro lugar, criamos o limite eficiente executando um loop. Em cada ciclo, consideramos um conjunto diferente de pesos atribuídos aleatoriamente para os ativos em nosso portfólio e calculamos o retorno e a volatilidade para essa combinação de pesos.

Para isso criamos 3 listas vazias, um para armazenar devoluções, outro para armazenar a volatilidade e o último para armazenar os pesos do portfólio.

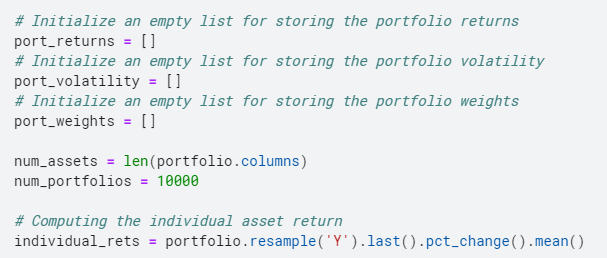
Depois de criarmos as listas, nós geramos aleatoriamente os pesos de nossos ativos repetidamente, então normalizamos a ponderação para adicionar 1. Em seguida, calculamos os retornos da mesma forma que calculamos acima. Subseqüentemente, Calculamos a variância da carteira e, em seguida, tiramos a raiz quadrada e, em seguida, anualizamos para obter a volatilidade, a mediro "medir" É um conceito fundamental em várias disciplinas, que se refere ao processo de quantificação de características ou magnitudes de objetos, Fenômenos ou situações. Na matemática, Usado para determinar comprimentos, Áreas e volumes, enquanto nas ciências sociais pode se referir à avaliação de variáveis qualitativas e quantitativas. A precisão da medição é crucial para obter resultados confiáveis e válidos em qualquer pesquisa ou aplicação prática.... de riesgo para nuestra cartera.

Agora agregamos os dados em um dicionário e, em seguida, criamos um quadro de dados para ver a combinação de pesos de ativos e os retornos e volatilidade correspondentes que eles geram.

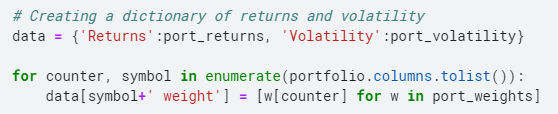
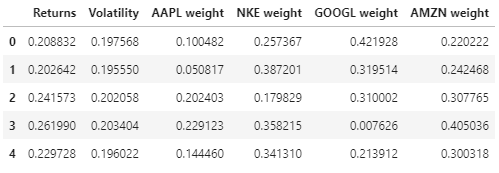
Aqui está uma prévia dos dados de lucratividade, volatilidade e pesos da carteira.

Agora temos tudo conosco para entrar na última volta desta corrida e encontrar o conjunto ideal de pesos!!

Nós plotamos a Volatilidade contra os retornos que calculamos anteriormente, isso nos dará a fronteira eficiente que queríamos criar no início deste artigo.

E aqui vamos nós!!

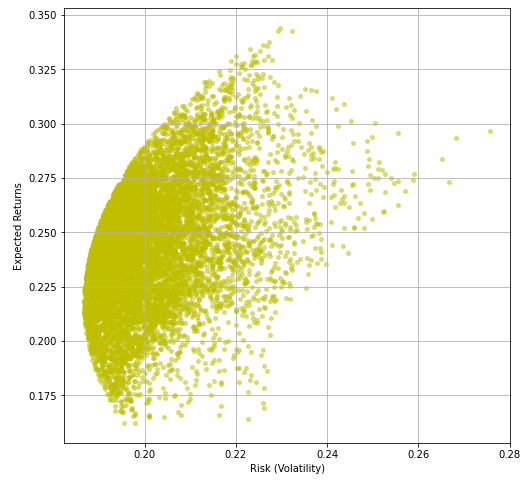
Agora que temos a Fronteira Eficiente conosco, vamos encontrar os pesos ideais.

Podemos otimizar o uso de vários métodos, conforme descrito abaixo:

• Portfólio com volatilidade mínima (risco)
• Portfólio ideal (Razão máxima de Sharpe)
• Retorno máximo em nível de risco; Risco mínimo em um nível esperado de retorno; Portfólio com a maior proporção de Sortino

Neste artigo, irei otimizar por meio das duas primeiras abordagens. No terceiro segmento, o ‘Retorno máximo em um nível de risco’ e o ‘Risco mínimo em um nível esperado de retorno’ eles são bastante simples, mientras que el que se basa en el índiceo "Índice" É uma ferramenta fundamental em livros e documentos, que permite localizar rapidamente as informações desejadas. Geralmente, é apresentado no início de um trabalho e organiza os conteúdos de forma hierárquica, incluindo capítulos e seções. Sua correta preparação facilita a navegação e melhora a compreensão do material, tornando-se um recurso essencial para estudantes e profissionais de várias áreas.... de Sortino es similar al índice de Sharpe.

1. Volatilidade mínima

Para encontrar a combinação de volatilidade mínima, selecionamos a linha em nosso quadro de dados que corresponde à variância mínima e encontramos essa linha usando a função .idxmin (). O código para fazer o mesmo é mostrado abaixo:

Os pesos que obtemos disso são:

Agora, descubra onde está o ponto mais baixo de volatilidade na curva acima. A resposta é exibida no final! Mas não trapaceie!

2. Maior relação de nitidez

O índice de Sharpe é o retorno médio obtido acima da taxa livre de risco por unidade de volatilidade ou risco total.. A fórmula usada para calcular o índice de Sharpe é fornecida abaixo:

Relação de nitidez = (R_pag – R_F)/ DAKOTA DEL ON_pag

Onde,

• R_pag é o retorno do portfólio
• R_F é a taxa livre de risco
• Dakota del sur_pag é o desvio padrão dos retornos do portfólio

O código para calcular o portfólio ideal, quer dizer, a carteira com o maior índice Sharpe, mostrado abaixo:

A seguir, Os pesos da carteira que fornecem o índice Sharpe mais alto são mostrados:

Descubra onde está o ponto de relacionamento Sharpe mais alto na curva acima. A resposta é mostrada abaixo! Mais uma vez, não faça armadilhas!

Conforme prometido, aqui está a resposta às duas perguntas acima!!

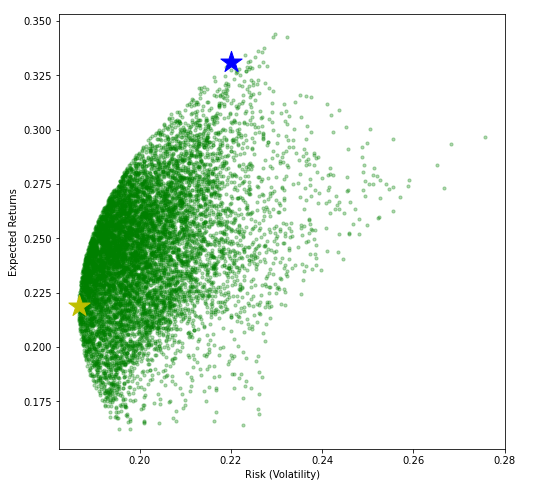
A estrela azul corresponde ao ponto de relacionamento de Sharpe mais alto e a estrela amarela corresponde ao ponto de volatilidade mínima.

Agora, antes de terminar este artigo, Eu encorajo você a encontrar o portfólio de Retorno Máximo em um nível de risco 'e’ Risco mínimo em um nível de lucratividade esperado 'e marque-os no gráfico anterior.

Além de usar a relação de Sharpe, também podemos otimizar o portfólio usando o relacionamento Sortino.

Dando um breve sobre isso:

a Relacionamento Sortino é uma variação do índice de Sharpe que diferencia a volatilidade prejudicial da volatilidade geral geral, usando o desvio padrão do ativo de retornos negativos da carteira (desvio para baixo) em vez do desvio padrão total dos retornos do portfólio. O índice Sortino pega o retorno de um ativo ou carteira e subtrai a taxa livre de risco, e, em seguida, divida esse valor pela tendência de queda do ativo. [Investopedia]

Taxa de classificação = (R_pag – r_F)/ DAKOTA DEL OND

Onde,

• R_pag é o retorno do portfólio
• r_F é a taxa livre de risco
• Dakota del surD é o desvio padrão da deficiência

Caso você tenha problemas para implementar ou compreender o 3 métodos de otimização que descrevi acima, escreva-me em [e-mail protegido] | [e-mail protegido] | ou entre em contato com o LinkedIn em https://www.linkedin.com/in/parth-tyagi-4b867452/

Nota sobre o autor: Parth Tyagi está atualmente estudando PGDBA no IIM Calcutta, IIT Kharagpur & Instituto de Estatística Indiano-Calcutá e concluiu o B.Tech do IIT Delhi. Tem ~ 4 anos de experiência de trabalho em análises avançadas.

Relacionado