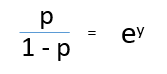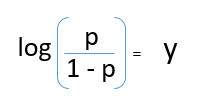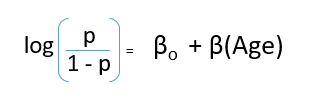Regressão logística R | Introdução à regressão logística

Visão geral

• Obtenha uma introdução à regressão logística usando R e Python
• A regressão logística é um algoritmo de classificação popular usado para prever um resultado binário.
• Existem várias métricas para avaliar um modelo de regressão logística, como matriz de confusão, curva AUC-ROC, etc.

Introdução

Cada algoritmo de aprendizado de máquina funciona melhor sob um determinado conjunto de condições. Certifique-se de que seu algoritmo se encaixa nas suposições / requisitos garantem desempenho superior. Nenhum algoritmo pode ser usado em qualquer condição. Por exemplo: Você já tentou usar regressão linear em uma variávelEm estatística e matemática, uma "variável" é um símbolo que representa um valor que pode mudar ou variar. Existem diferentes tipos de variáveis, e qualitativo, que descrevem características não numéricas, e quantitativo, representando quantidades numéricas. Variáveis são fundamentais em experimentos e estudos, uma vez que permitem a análise de relações e padrões entre diferentes elementos, facilitando a compreensão de fenômenos complexos.... dependiente categórica? Nem tente! Porque você não será apreciado por obter valores extremamente baixos da estatística R² e F ajustada.

Em vez de, em tais situações, você deve tentar usar algoritmos como regressão logística, Árvores de decisão, SVM, Floresta aleatória, etc. Para uma visão geral rápida desses algoritmos, Vou recomendar a leitura: Noções básicas de algoritmo de aprendizado de máquina.

Com esta postagem, Eu forneço a você conhecimentos úteis sobre regressão logística em R. Depois de dominar a regressão linear, este é o próximo passo natural em sua jornada. Também é fácil de aprender e implementar, mas você deve conhecer a ciência por trás deste algoritmo.

Tentei explicar esses conceitos da maneira mais simples possível. Comecemos.

O que é regressão logística?

A regressão logística é um algoritmo de classificação. Usado para prever um resultado binário (1/0, sim / Não, Verdade / Falso) dado um conjunto de variáveis ​​independentes. Para representar um resultado binário / categórico, nós usamos variáveis ​​fictícias. Você também pode pensar na regressão logística como um caso especial de regressão linear quando a variável de resultado é categórica., onde usamos o logaritmo das probabilidades como a variável dependente. Em palavras simples, prevê a probabilidade de ocorrência de um evento ajustando os dados a uma função logit.

Derivação da equação de regressão logística

A regressão logística faz parte de uma classe maior de algoritmos conhecida como modelo linear generalizado. (glm). Sobre 1972, Nelder e Wedderburn propuseram este modelo em um esforço para fornecer um meio de usar a regressão linear para problemas que não eram diretamente adequados para a aplicação da regressão linear.. De fato, propôs uma classe de modelos diferentes (regressão linear, ANOVA, Regressão de Poisson, etc.) que incluiu regressão logística como um caso especial.

A equação fundamental do modelo linear generalizado é:

g(E(e)) = α + βx1 + γx2

Aqui, g () é a função de link, E (e) é a expectativa da variável alvo e α + βx1 + γx2 é o preditor linear (uma, b, γ a ser previsto). O papel da função de link é “link” a expectativa de y para o preditor linear.

Pontos importantes

1. O GLM não assume uma relação linear entre as variáveis ​​dependentes e independentes. Porém, assume uma relação linear entre a função de ligação e as variáveis ​​independentes no modelo logit.
2. A variável dependente não precisa ser distribuída normalmente.
3. Não usa OLS (Mínimo quadrado comum) para la estimación de parametroso "parametros" são variáveis ou critérios usados para definir, medir ou avaliar um fenômeno ou sistema. Em vários domínios, como a estatística, Ciência da Computação e Pesquisa Científica, Os parâmetros são essenciais para estabelecer normas e padrões que orientam a análise e interpretação dos dados. Sua seleção e manuseio adequados são cruciais para obter resultados precisos e relevantes em qualquer estudo ou projeto..... Em vez de, usa estimativa de máxima verossimilhança (MLE).
4. Os erros devem ser independentes, mas não normalmente distribuídos.

Vamos entender mais com um exemplo:

Recebemos uma amostra de 1000 clientes. Precisamos prever a probabilidade de um cliente comprar (e) uma revista particular ou não. Como você pode ver, temos uma variável de resultado categórica, vamos usar regressão logística.

Para começar com regressão logística, Vou escrever primeiro a equação de regressão linear simples com a variável dependente incluída em uma função de link:

                           g(e) = βo + b(Era)         ---- (uma)

Observação: Para facilitar a compreensão, Eu considerei ‘Idade’ como variável independente.

Na regressão logística, estamos apenas preocupados com a probabilidade da variável dependente do resultado (sucesso ou fracasso). Como descrito acima, g () é a função de link. Esta função é estabelecida por duas coisas: probabilidade de sucesso (p) e probabilidade de falha (1-p). p deve atender aos seguintes critérios:

1. Deve ser sempre positivo (desde p> = 0)
2. Deve ser sempre menor que igual a 1 (desde p <= 1)

Agora, nós simplesmente iremos satisfazer estes 2 condições e chegar ao cerne da regressão logística. Para definir a função de link, denotaremos g () com 'p’ inicialmente e eventualmente acabaremos derivando esta função.

Uma vez que a probabilidade deve ser sempre positiva, vamos colocar a equação linear na forma exponencial. Para qualquer valor de inclinação e variável dependente, o expoente desta equação nunca será negativo.

p = exp(βo + b(Era)) = e ^(βo + b(Era))    ------- (b)

Para que a probabilidade seja menor que 1, devemos dividir p por um número maior que p. Isso pode ser feito simplesmente por:

p = exp(βo + b(Era)) / exp(βo + b(Era)) + 1   = e ^(βo + b(Era)) / e ^(βo + b(Era)) + 1    ----- (c)

Usando (uma), (b) e (c), podemos redefinir a probabilidade como:

              p = e ^ y / 1 + e ^ y           --- (d)

Onde p é a probabilidade de sucesso. Está (d) é a função Logit

Se p é a probabilidade de sucesso, 1-p será a probabilidade de falha que pode ser escrita como:

q = 1 - p = 1 - (e ^ y / 1 + e ^ y)    --- (e)

Onde q é a probabilidade de falha

Ao dividir, (d) / (e), nós obtemos,

Depois de tirar o recorde de ambos os lados, nós obtemos,

registro (p / 1-p) é a função de link. A transformação logarítmica da variável de resultado nos permite modelar uma associação não linear de forma linear.

Depois de substituir o valor de y, nós conseguiremos:

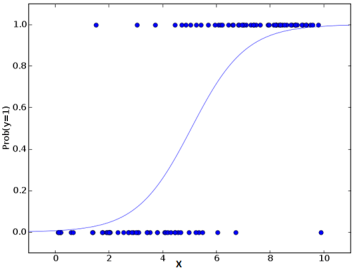
Esta é a equação usada na Regressão Logística. Aqui (p / 1-p) é a razão estranha. Quando o logaritmo da razão ímpar é determinado como positivo, a probabilidade de sucesso é sempre maior do que 50%. Abaixo está um gráfico típico de modelo logístico. Você pode ver que a probabilidade nunca cai abaixo de 0 e acima 1.

Desempenho do modelo de regressão logística

Para avaliar o desempenho de um modelo de regressão logística, devemos considerar algumas métricas. Independentemente da ferramenta (SAS, R, Pitão) onde eu trabalharia, olho sempre:

1. AIC (Critérios de informação de Akaike) – A métrica análoga de R2 ajustado em regressão logística é AIC. AIC é a medida de ajuste que penaliza o modelo pelo número de coeficientes do modelo. Portanto, sempre preferimos o modelo com um valor mínimo de AIC.

2. Desvio nulo e desvio residual – O desvio nulo indica a resposta prevista por um modelo com nada mais do que uma interseção. Abaixe o valor, melhor o modelo. O desvio residual indica a resposta prevista por um modelo ao adicionar variáveis ​​independentes. Abaixe o valor, melhor o modelo.

3. Matriz de confusão: Não é nada mais do que uma representação tabular dos valores reais versus os previstos.. Isso nos ajuda a encontrar a precisão do modelo e evitar overfitting.. É assim que parece:

Fonte: (plugue – n – pontuação)

Você pode calcular o precisão do seu modelo com:

Da matriz de confusão, especificidade e sensibilidade podem ser derivadas conforme ilustrado abaixo:

A especificidade e a sensibilidade desempenham um papel crucial na derivação da curva ROC..

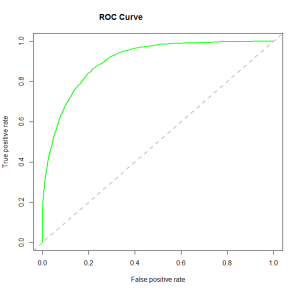
4. Curva ROC: A característica operacional do receptor (ROC) resume o desempenho do modelo avaliando as compensações entre a taxa de verdadeiros positivos (sensibilidade) e a taxa de falsos positivos (1 especificidade). Para representar graficamente ROC, é aconselhável assumir p> 0.5 já que estamos mais preocupados com a taxa de sucesso. ROC resume o poder preditivo para todos os valores possíveis de p> 0.5. A área sob a curva (AUC), denominada índiceo "Índice" É uma ferramenta fundamental em livros e documentos, que permite localizar rapidamente as informações desejadas. Geralmente, é apresentado no início de um trabalho e organiza os conteúdos de forma hierárquica, incluindo capítulos e seções. Sua correta preparação facilita a navegação e melhora a compreensão do material, tornando-se um recurso essencial para estudantes e profissionais de várias áreas.... precisão (UMA) ou índice de concordância, é uma métrica de desempenho perfeita para a curva ROC. Quanto maior for a área sob a curva, melhor será o poder preditivo do modelo. Abaixo está uma amostra de curva ROC. O ROC de um modelo preditivo perfeito tem TP igual a 1 e FP igual a 0. Esta curva tocará o canto superior esquerdo do gráfico..

Observação: Para desempenho de modelo, você também pode considerar a função de probabilidade. É assim chamado porque seleciona os valores dos coeficientes que maximizam a probabilidade de explicar os dados observados. Indica a qualidade do ajuste quando seu valor se aproxima de um e um ajuste insatisfatório dos dados quando seu valor se aproxima de zero.

Modelo de regressão logística em R e Python

O código R é fornecido abaixo, mas se você é um usuário python, aqui está uma janela de código incrível para construir o seu modelo de regressão logística. Não há necessidade de abrir Jupyter, você pode fazer tudo aqui:

Levando em conta a disponibilidade, Eu construí este modelo sobre o nosso problema de prática: o conjunto de dados Dressify. Você pode baixá-lo aqui.

Sem se aprofundar na engenharia de recursos, aqui é o simples script modelo de regressão logística:

setwd('C:/Usuários/manish/Desktop/dressdata')

#load data
train <- read.csv('Train_Old.csv')

#create training and validation data from given data
install.packages('caTools')
biblioteca(caTools)

set.seed(88)
dividir <- sample.split(trem$Recomendado, SplitRatio = 0.75)

#get training and test data
dresstrain <- subconjunto(Comboio, split == TRUE)
dresstest <- subconjunto(Comboio, split == FALSO)

#logistic regression model
model <- glm (Recomendado ~ .-ID, dados = dresstrain, família = binômio)
resumo(modelo)

prever <- prever(modelo, tipo ="resposta")

#confusion matrix
table(dresstrain$Recomendado, prever > 0.5)

#ROCR Curve
library(ROCR)
ROCRpred <- predição(prever, dresstrain$Recomendado)
ROCRperf <- arte performance(ROCRpred, 'tpr','fpr')
enredo(ROCRperf, colorize = TRUE, text.adj = c(-0.2,1.7))

#plot glm
library(ggplot2)
ggplot(dresstrain, aes(x=Classificação, y=Recomendado)) + geom_point() + 
stat_smooth(método= método="glm", familia ="binômio", se=FALSO)

Esses dados exigem muita limpeza e engenharia de recursos. O escopo deste artigo me impediu de manter o exemplo focado na construção do modelo de regressão logística.. Esses dados são acessível para praticar. Eu recomendo que você trabalhe neste problema. Há muito o que aprender..

Notas finais

A estas alturas, você já vai saber a ciência por trás da regressão logística. Já vi muitas vezes que as pessoas sabem o uso deste algoritmo sem ter conhecimento sobre seus conceitos principais.. Eu fiz o meu melhor para explicar esta parte da forma mais simples possível.. O exemplo anterior mostra apenas o esqueleto do uso de regressão logística em R. Antes de realmente chegar a este estágio, você deve investir seu tempo crucial na engenharia de recursos.

O que mais, Eu recomendo que você trabalhe neste conjunto de problemas. Você exploraria coisas que pode não ter enfrentado antes.

Eu perdi algo importante? Você acha útil este artigo? Compartilhe suas opiniões / pensamentos na seção de comentários abaixo.

Se você gostou do que acabou de ler e deseja continuar seu aprendizado sobre análise, inscreva-se em nossos e-mails, Siga-nos no Twitter ou como o nosso página do Facebook.

Relacionado