Vamos começar fazendo uma breve declaração do problema.
Declaração do problema: criar um modelo de regressão linear simples para prever o aumento de salário usando anos de experiência.
Comece importando as bibliotecas necessárias
Bibliotecas obrigatórias são pandas, NumPy para trabalhar com frames de dados, matplotlib, marítimo para visualizações e sklearn, modelos de estatísticas para construir modelos de regressão.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
from scipy import stats
from scipy.stats import probplot
import statsmodels.api as sm
import statsmodels.formula.api as smf
from sklearn import preprocessing
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_scoreAssim que terminarmos de importar bibliotecas, nós criamos um quadro de dados do pandas a partir do arquivo CSV
df = pd.read_csv(“Salary_Data.csv”)
Executar EDA (Análise exploratória de dados)
As etapas básicas do EDA são:
- Identifique o número de recursos ou colunas
- Identifique as características ou colunas
- Identifique o tamanho do conjunto de dados
- Identificação dos tipos de dados das características
- Verificar se o conjunto de dados tem células vazias
- Identifique o número de células vazias por características ou colunas
- Tratamento de valores ausentes e outliers
- Codificação de variáveis categóricas
- Análise gráfica univariada, bivariado
- NormalizaçãoA padronização é um processo fundamental em várias disciplinas, que busca estabelecer padrões e critérios uniformes para melhorar a qualidade e a eficiência. Em contextos como engenharia, Educação e administração, A padronização facilita a comparação, Interoperabilidade e compreensão mútua. Ao implementar normas, a coesão é promovida e os recursos são otimizados, que contribui para o desenvolvimento sustentável e a melhoria contínua dos processos.... y escalado
len(df.columns) # identificar o número de recursosdf.columns # Identificar os recursos
df.shape # identify the size of of the datasetUn "dataset" o conjunto de datos es una colección estructurada de información, que puede ser utilizada para análisis estadísticos, machine learning o investigación. Los datasets pueden incluir variables numéricas, categóricas o textuales, y su calidad es crucial para obtener resultados fiables. Su uso se extiende a diversas disciplinas, como la medicina, la economía y la ciencia social, facilitando la toma de decisiones informadas y el desarrollo de modelos predictivos....df.dtypes # identify the datatypes of the featuresdf.isnull().values.any() # checking if dataset has empty cellsdf.isnull().sum() # identify the number of empty cellsNosso conjunto de dados tem duas colunas: Anos de experiência, Salário. E ambos são tipo de dados flutuantes. Tenho 30 registros e não temos nulos ou outliers em nosso conjunto de dados.
Análise gráfica univariada
Para análise univariada, tenho Histograma, gráfico de densidade, enredo de caixa o rabeca, e Gráfico QQ normal. Eles nos ajudam a entender a distribuição de pontos de dados e a presença de outliers.
uma diagrama de violinoO diagrama de violino é uma representação gráfica que combina características de um boxplot e um gráfico de densidade. Usado para visualizar a distribuição de um conjunto de dados, mostrando a mediana e a variabilidade através de sua forma, que se assemelha a um violino. Este tipo de gráfico é muito útil na análise estatística, ya que permite comparar múltiples distribuciones de forma clara y efectiva.... es un método para trazar datos numéricos. É semelhante a um gráfico de caixa, com a adição de um diagrama de densidade de grãos girado em cada lado.
Código Python:
# Histogram
# We can use either plt.hist or sns.histplot
plt.figure(figsize=(20,10))
plt.subplot(2,4,1)
plt.hist(df['YearsExperience'], density=False)
plt.title("Histogram of 'YearsExperience'")
plt.subplot(2,4,5)
plt.hist(df['Salary'], density=False)
plt.title("Histogram of 'Salary'")
# Density plot
plt.subplot(2,4,2)
sns.distplot(df['YearsExperience'], kde=True)
plt.title("Density distribution of 'YearsExperience'")
plt.subplot(2,4,6)
sns.distplot(df['Salary'], kde=True)
plt.title("Density distribution of 'Salary'")
# boxplot or violin plot
# A violin plot is a method of plotting numeric data. It is similar to a box plot,
# with the addition of a rotated kernel density plot on each side
plt.subplot(2,4,3)
# plt.boxplot(df['YearsExperience'])
sns.violinplot(df['YearsExperience'])
# plt.title("Boxlpot of 'YearsExperience'")
plt.title("Violin plot of 'YearsExperience'")
plt.subplot(2,4,7)
# plt.boxplot(df['Salary'])
sns.violinplot(df['Salary'])
# plt.title("Boxlpot of 'Salary'")
plt.title("Violin plot of 'Salary'")
# Normal Q-Q plot
plt.subplot(2,4,4)
probplot(df['YearsExperience'], plot=plt)
plt.title("Q-Q plot of 'YearsExperience'")
plt.subplot(2,4,8)
probplot(df['Salary'], plot=plt)
plt.title("Q-Q plot of 'Salary'")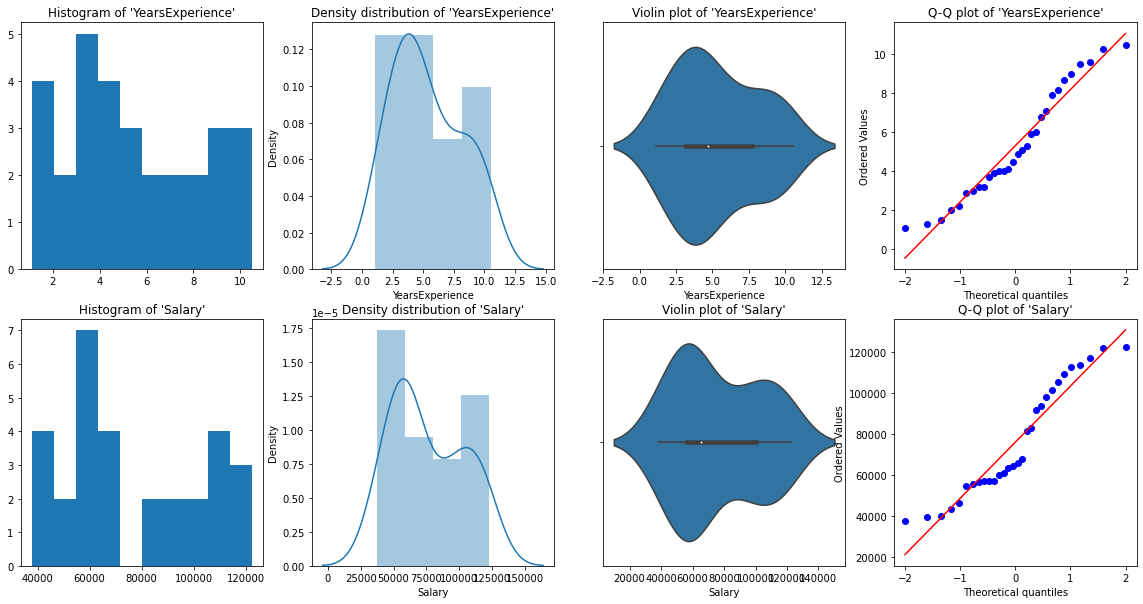
Das representações gráficas acima, podemos dizer que não há outliers em nossos dados, e YearsExperience looks like normally distributed, and Salary doesn't look normal. Podemos verificar isso usando Shapiro Test.
Código Python:
# Def a function to run Shapiro test
# Defining our Null, Alternate Hypothesis
Ho = 'Data is Normal'
Ha="Data is not Normal"
# Defining a significance value
alpha = 0.05
def normality_check(df):
for columnName, columnData in df.iteritems():
print("Shapiro test for {columnName}".format(columnName=columnName))
res = stats.shapiro(columnData)
# print(res)
pValue = round(res[1], 2)
# Writing condition
if pValue > alpha:
print("pvalue = {pValue} > {alpha}. We fail to reject Null Hypothesis. {Ho}".format(pValue=pValue, alpha=alpha, Ho=Ho))
else:
print("pvalue = {pValue} <= {alpha}. We reject Null Hypothesis. {Ha}".format(pValue=pValue, alpha=alpha, Ha=Ha))
# Drive code
normality_check(df)Nosso instinto gráfico estava correto. Os anos de experiência são normalmente distribuídos e o salário não é normalmente distribuído.
Exibição bivariada
para dados numéricos vs dados numéricos, podemos desenhar os seguintes gráficos
- Gráfico de dispersão
- Gráfico de linha
- Mapa de calor para correlação
- Parcela conjunta
Código Python para varias parcelas:
# Scatterplot & Line plots
plt.figure(figsize=(20,10))
plt.subplot(1,3,1)
sns.scatterplot(data=df, x="YearsExperience", y="Salary", hue="YearsExperience", alpha=0.6)
plt.title("Scatter plot")
plt.subplot(1,3,2)
sns.lineplot(data=df, x="YearsExperience", y="Salary")
plt.title("Line plot of YearsExperience, Salary")
plt.subplot(1,3,3)
sns.lineplot(data=df)
plt.title('Line Plot')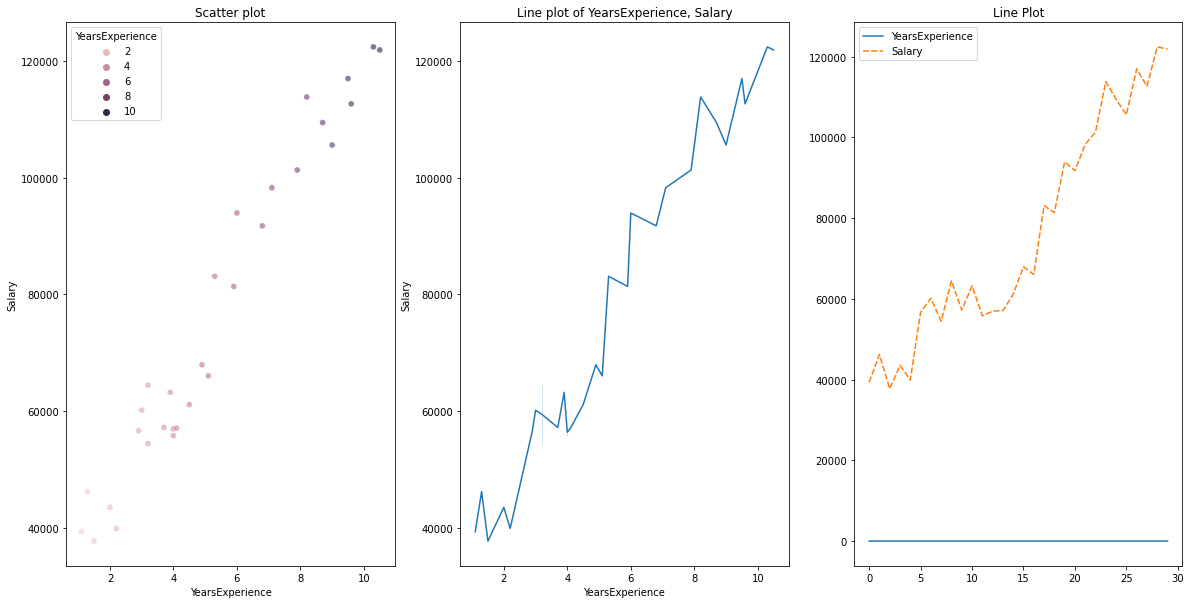
# heatmap
plt.figure(figsize=(10, 10))
plt.subplot(1, 2, 1)
sns.heatmap(data=df, cmap="YlGnBu", annot = True)
plt.title("Heatmap using seaborn")
plt.subplot(1, 2, 2)
plt.imshow(df, cmap ="YlGnBu")
plt.title("Heatmap using matplotlib")
# Joint plot
sns.jointplot(x = "YearsExperience", y = "Salary", kind = "reg", data = df)
plt.title("Joint plot using sns")
# kind can be hex, kde, scatter, reg, hist. When kind='reg' it shows the best fit line.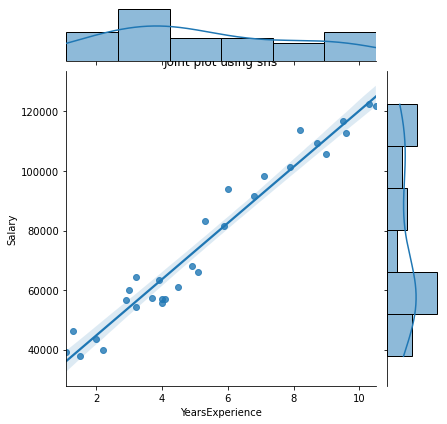
Verifique se existe alguma correlação entre as variáveis usando df.corr ()
print("Correlation: "+ 'n', df.corr()) # 0.978 which is high positive correlation
# Draw a heatmap for correlation matrix
plt.subplot(1,1,1)
sns.heatmap(df.corr(), annot=True)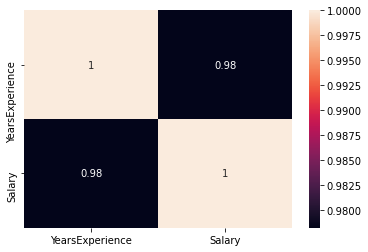
correlação = 0,98, que é uma correlação positiva alta. Esto significa que la variávelEm estatística e matemática, uma "variável" é um símbolo que representa um valor que pode mudar ou variar. Existem diferentes tipos de variáveis, e qualitativo, que descrevem características não numéricas, e quantitativo, representando quantidades numéricas. Variáveis são fundamentais em experimentos e estudos, uma vez que permitem a análise de relações e padrões entre diferentes elementos, facilitando a compreensão de fenômenos complexos.... dependiente aumenta a medida que aumenta la variable independiente.
Normalização
Como podemos ver, há uma grande diferença entre os valores das colunas YearsExperience, Salário. Podemos usar Normalization para alterar os valores das colunas numéricas no conjunto de dados para usar uma escala comum, sem distorcer as diferenças nas faixas de valor ou perder informações.
Nós usamos sklearn.preprocessing.Normalize para normalizar nossos dados. Retorna valores entre 0 e 1.
# Create new columns for the normalized values
df['Norm_YearsExp'] = preprocessing.normalize(df[['YearsExperience']], axis=0)
df['Norm_Salary'] = preprocessing.normalize(df[['Salary']], axis=0)
df.head()Regressão linear usando scikit-learn
LinearRegression(): LinearRegression está em conformidade com um modelo linear com coeficientes β = (β1, ..., βp) para minimizar a soma residual dos quadrados entre os alvos observados no conjunto de dados e os alvos previstos pela aproximação linear.
def regression(df):
# defining the independent and dependent features
x = df.iloc[:, 1:2]
y = df.iloc[:, 0:1]
# print(x,y)
# Instantiating the LinearRegression object
regressor = LinearRegression()
# Training the model
regressor.fit(x,y)
# Checking the coefficients for the prediction of each of the predictor
print('n'+"Coeff of the predictor: ",regressor.coef_)
# Checking the intercept
print("Intercept: ",regressor.intercept_)
# Predicting the output
y_pred = regressor.predict(x)
# print(y_pred)
# Checking the MSE
print("Mean squared error(MSE): %.2f" % mean_squared_error(y, y_pred))
# Checking the R2 value
print("Coefficient of determination: %.3f" % r2_score(y, y_pred)) # Evaluates the performance of the model # says much percentage of data points are falling on the best fit line
# visualizing the results.
plt.figure(figsize=(18, 10))
# Scatter plot of input and output values
plt.scatter(x, y, color="teal")
# plot of the input and predicted output values
plt.plot(x, regressor.predict(x), color="Red", linewidth=2 )
plt.title('Simple Linear Regression')
plt.xlabel('YearExperience')
plt.ylabel('Salary')
# Driver code
regression(df[['Salary', 'YearsExperience']]) # 0.957 accuracy
regression(df[['Norm_Salary', 'Norm_YearsExp']]) # 0.957 accuracyAlcançamos uma precisão de 95,7% con scikit-learn, pero no hay mucho margemMargem é um termo usado em uma variedade de contextos, como contabilidade, Economia e impressão. Em contabilidade, refere-se à diferença entre receitas e custos, que permite avaliar a rentabilidade de um negócio. No domínio da publicação, A margem é o espaço em branco ao redor do texto em uma página, que facilita a leitura e proporciona uma apresentação estética. Seu correto manejo é essencial.. para comprender la información detallada sobre la relevancia de las características de este modelo. Então, vamos construir um modelo usando statsmodels.api, statsmodels.formula.api
Regressão linear usando statsmodel.formula.api (smf)
Os preditores em statsmodels.formula.api devem ser listados individualmente. E neste método, uma constante é automaticamente adicionada aos dados.
def smf_ols(df):
# defining the independent and dependent features
x = df.iloc[:, 1:2]
y = df.iloc[:, 0:1]
# print(x)
# train the model
model = smf.ols('y~x', data=df).fit()
# print model summary
print(model.summary())
# Predict y
y_pred = model.predict(x)
# print(type(y), type(y_pred))
# print(y, y_pred)
y_lst = y.Salary.values.tolist()
# y_lst = y.iloc[:, -1:].values.tolist()
y_pred_lst = y_pred.tolist()
# print(y_lst)
data = [y_lst, y_pred_lst]
# print(data)
res = pd.DataFrame({'Actuals':data[0], 'Predicted':data[1]})
# print(res)
plt.scatter(x=res['Actuals'], y=res['Predicted'])
plt.ylabel('Predicted')
plt.xlabel('Actuals')
res.plot(kind='bar',figsize=(10,6))
# Driver code
smf_ols(df[['Salary', 'YearsExperience']]) # 0.957 accuracy
# smf_ols(df[['Norm_Salary', 'Norm_YearsExp']]) # 0.957 accuracy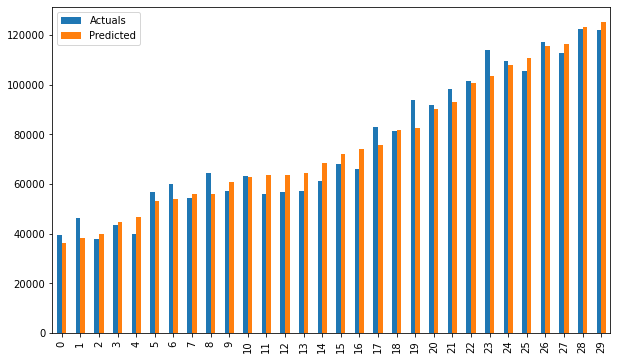
Regressão usando statsmodels.api
Não é mais necessário listar preditores individualmente.
statsmodels.regression.linear_model.OLS (até, exog)
endogé a variável dependenteexogé a variável independente. Uma interceptação não é incluída por padrão e deve ser adicionada pelo usuário (usando add_constant).
# Create a helper function
def OLS_model(df):
# defining the independent and dependent features
x = df.iloc[:, 1:2]
y = df.iloc[:, 0:1]
# Add a constant term to the predictor
x = sm.add_constant(x)
# print(x)
model = sm.OLS(y, x)
# Train the model
results = model.fit()
# print('n'+"Confidence interval:"+'n', results.conf_int(alpha=0.05, cols=None)) #Returns the confidence interval of the fitted parameters. The default alpha=0.05 returns a 95% confidence interval.
print('n'"Model parameters:"+'n',results.params)
# print the overall summary of the model result
print(results.summary())
# Driver code
OLS_model(df[['Salary', 'YearsExperience']]) # 0.957 accuracy
OLS_model(df[['Norm_Salary', 'Norm_YearsExp']]) # 0.957 accuracyAlcançamos uma precisão de 95,7%, o que é muito bom 🙂
¿Qué dice la tabla de resumeno "tabla de resumen" es una herramienta eficaz que condensa información clave de un tema específico en un formato visual y accesible. Utilizada en diversos campos, como la educación y la investigación, facilita la comprensión y el análisis de datos. Su estructura permite a los usuarios identificar rápidamente los puntos esenciales, promoviendo una mejor retención del conocimiento y una comparación más sencilla entre diferentes conceptos o variables.... do modelo? 😕
É sempre importante entender certos termos na tabela de resumo do modelo de regressão para que possamos saber o desempenho do nosso modelo e a relevância das variáveis de entrada.
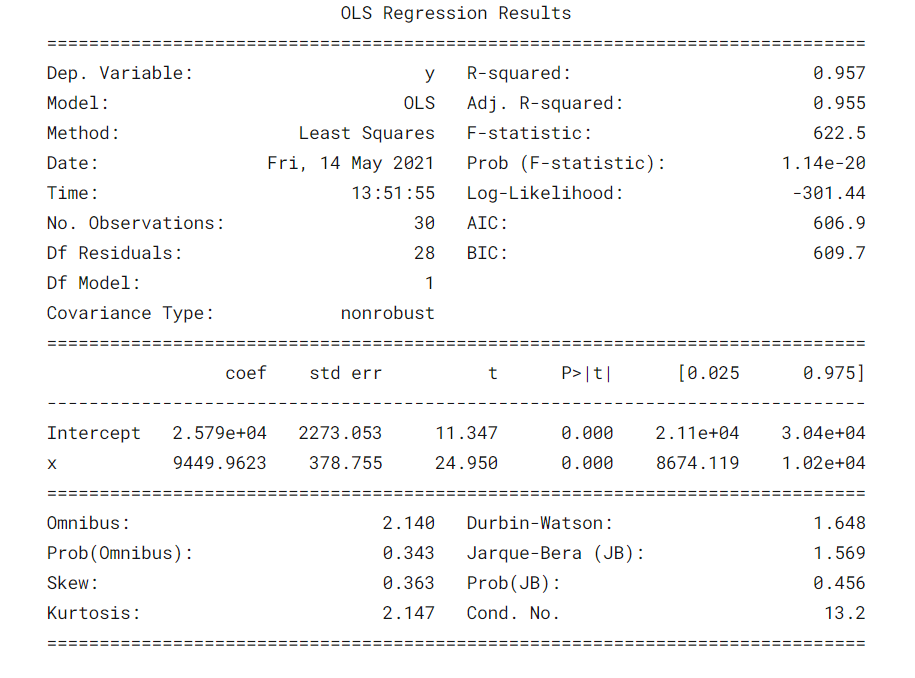
Algum parametroso "parametros" são variáveis ou critérios usados para definir, medir ou avaliar um fenômeno ou sistema. Em vários domínios, como a estatística, Ciência da Computação e Pesquisa Científica, Os parâmetros são essenciais para estabelecer normas e padrões que orientam a análise e interpretação dos dados. Sua seleção e manuseio adequados são cruciais para obter resultados precisos e relevantes em qualquer estudo ou projeto.... importantes que deben tenerse en cuenta son el valor de R cuadrado, Adj. Valor R-quadrado, Estatística F, prob (Estatística F), coeficiente de interceptação e variáveis de entrada, p> | t |.
- R-quadrado é o coeficiente de determinação. Uma medida estatística que diz que uma grande parte dos pontos de dados estão na linha de melhor ajuste. Um valor de R ao quadrado mais próximo de 1 para um modelo se encaixar bem.
- Adj. R-quadrado penaliza o valor de R-quadrado se continuarmos adicionando os novos recursos que não contribuem para a previsão do modelo. Si Adj. Valor de R ao quadrado <Valor R-quadrado, é um sinal de que temos preditores irrelevantes no modelo.
- La estadística F o prueba F nos ayuda a aceptar o rechazar la hipótese nulaA hipótese nula é um conceito fundamental em estatística que estabelece uma declaração inicial sobre um parâmetro populacional. Seu objetivo é ser testado e, se refutado, nos permite aceitar a hipótese alternativa. Essa abordagem é essencial na pesquisa científica, pois fornece uma estrutura para avaliar evidências empíricas e tomar decisões baseadas em dados. Sua formulação e análise são cruciais em estudos estatísticos..... Compare o modelo somente de interceptação com nosso modelo com recursos. A hipótese nula é “todos os coeficientes de regressão são iguais a zero e isso significa que ambos os modelos são iguais”. A hipótese alternativa é 'interceptar o único modelo é pior do que o nosso modelo, o que significa que nossos coeficientes adicionados melhoraram o desempenho do modelo. Se prob (Estatística F) <0.05 e a estatística F é um valor alto, rejeitamos a hipótese nula. Isso significa que há uma boa relação entre as variáveis de entrada e saída.
- coef exibe os coeficientes estimados das características de entrada correspondentes
- O teste T fala sobre a relação entre a saída e cada uma das variáveis de entrada individualmente. A hipótese nula é 'o coeficiente de uma característica de entrada é 0'. A hipótese alternativa é 'o coeficiente de uma característica de entrada não é 0'. If pvalue 0.05.
Nós vamos, agora sabemos como tirar inferências importantes da tabela de resumo do modelo, então agora vamos olhar para os parâmetros do nosso modelo e avaliar nosso modelo.
No nosso caso, o valor de R ao quadrado (0,957) está perto de Adj. O valor de R ao quadrado (0,955) é um bom sinal de que as características de entrada estão contribuindo para o modelo preditor.
A estatística F é um número alto e p (Estatística F) é quase 0, o que significa que nosso modelo é melhor do que o modelo de interseção única.
O valor p do teste t para a variável de entrada é menor que 0.05, então há uma boa relação entre a variável de entrada e a variável de saída.
Portanto, concluímos dizendo que nosso modelo está funcionando bem ✔😊
Neste blog, Aprendemos o básico da Regressão Linear Simples (SLR), construir um modelo linear usando diferentes bibliotecas Python e fazer inferências a partir da tabela de resumo de modelos de estatísticas OLS.
Referências:
Interpretando a tabela de resumo do modelo de estatísticas OLS
Visualizações: Histograma, Gráfico de densidade, trama de violino, enredo de caixa, Gráfico QQ normal, Gráfico de dispersão, gráfico de linha, mapa de calor, conspiração conjunta
Veja o caderno completo do meu GitHub repositório.
Espero que este seja um blog informativo para iniciantes. Por favor, Vote se você achar isso útil 🙌 Seus comentários são muito apreciados. Boa aprendizagem !! 😎
A mídia mostrada neste artigo não é propriedade da DataPeaker e é usada a critério do autor.






