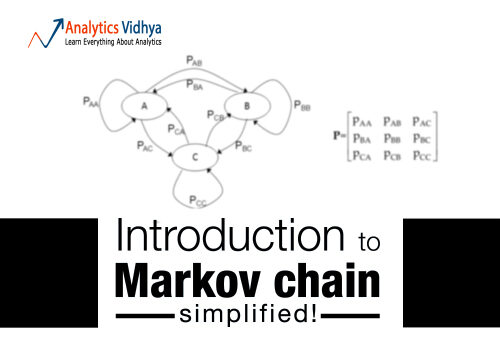
La cadena de Markov es un concepto simple que puede explicar los procesos en tiempo real más complicados. El reconocimiento de voz, los identificadores de texto, el reconocimiento de rutas y muchas otras herramientas de inteligencia artificial utilizan este principio simple llamado cadena de Markov de alguna forma. En este artículo ilustraremos lo fácil que es entender este concepto y lo implementaremos en R.
La cadena de Markov se basa en un principio de «falta de memoria». En otras palabras, el siguiente estado del proceso solo depende del estado anterior y no de la secuencia de estados. Esta simple suposición facilita el cálculo de la probabilidad condicional y permite que este algoritmo se aplique en varios escenarios. En este artículo nos limitaremos a una simple cadena de Markov. En problemas de la vida real, generalmente usamos el modelo de Markov latente, que es una versión muy evolucionada de la cadena de Markov. También hablaremos sobre una aplicación simple de la cadena de Markov en el próximo artículo.
Un caso de negocio sencillo
Coca-Cola y Pepsi son las únicas empresas en el país X. Una empresa de refrescos quiere vincularse con uno de estos competidores. Contratan a una empresa de investigación de mercado para averiguar cuál de las marcas tendrá una mayor participación de mercado después de 1 mes. Actualmente, Pepsi posee el 55% y Coke posee el 45% de la participación de mercado. A continuación se presentan las conclusiones extraídas por la empresa de investigación de mercado:
P (P-> P): Probabilidad de que un cliente se quede con la marca Pepsi durante un mes = 0,7
P (P-> C): probabilidad de que un cliente cambie de Pepsi a Coca-Cola durante un mes = 0,3
P (C-> C): Probabilidad de que un cliente se quede con la marca Coke durante un mes = 0.9
P (C-> P): Probabilidad de que un cliente cambie de Coca-Cola a Pepsi durante un mes = 0,1
Podemos ver claramente que los clientes tienden a quedarse con Coca-Cola, pero Coca-Cola actualmente tiene una participación de billetera más baja. Por lo tanto, no podemos estar seguros de la recomendación sin hacer algunos cálculos de transición.
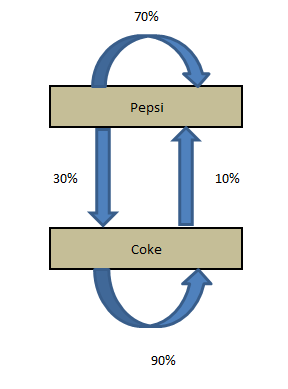
Diagrama de transición
Las cuatro declaraciones realizadas por la empresa de investigación se pueden estructurar en un diagrama de transición simple.
El diagrama simplemente muestra las transiciones y la cuota de mercado actual. Ahora, si queremos calcular la participación de mercado después de un mes, debemos hacer los siguientes cálculos:
Cuota de mercado (t + 1) de Pepsi = Cuota de mercado actual de Pepsi * P (P-> P) + Cuota de mercado actual de Coca-Cola * P (C-> P)
Participación de mercado (t + 1) de Coca-Cola = Participación de mercado actual de Coca-Cola * P (C-> C) + Participación de mercado actual de Pepsi * P (P-> C)
Estos cálculos se pueden hacer simplemente mirando la siguiente multiplicación de matrices:
Matriz de transición del estado actual X = estado final
Como podemos ver, vemos claramente que Pepsi, aunque tiene una cuota de mercado más alta ahora, tendrá una cuota de mercado más baja después de un mes. Este simple cálculo se llama cadena de Markov. Si la matriz de transición no cambia con el tiempo, podemos predecir la participación de mercado en cualquier momento futuro. Hagamos el mismo cálculo para 2 meses después.
Cálculos de estado estacionario
Además del caso de negocio que nos ocupa, la empresa de refrescos quiere reducir la brecha en la cuota de mercado de la empresa Coke y Pepsi a largo plazo. Esto les ayudará a enmarcar la estrategia de costos correcta mientras se lanzan a Coca-Cola. La participación de Pepsi seguirá bajando hasta un punto en que el número de clientes que abandonan Pepsi y el número de clientes que se adaptan a Pepsi es el mismo. Por lo tanto, necesitamos satisfacer las siguientes condiciones para encontrar las proporciones del estado estacionario:
Pepsi MS * 30% = Coca-Cola MS * 10% …………………………………………… ..1
Pepsi MS + Coca-Cola MS = 100% …………………………………………………… 2
4 * Pepsi MS = 100% => Pepsi MS = 25% y Coca-Cola MS = 75%
Formulemos un algoritmo para encontrar el estado estable. Después del estado estable, la multiplicación del estado inicial con la matriz de transición dará el estado inicial en sí. Por tanto, la matriz que puede satisfacer la siguiente condición serán las proporciones finales:
Estado inicial X Matriz de transición = Estado inicial
Al resolver la ecuación anterior, podemos encontrar la matriz de estado estable. La solución será la misma que [25%,75%].
Ahora resolvamos el ejemplo anterior en R.
Implementación en R
Paso 1: creación de una matriz de transición y una cadena de Markov de tiempo discreto
Producción
trans_mat [,1] [,2] [1,] 0.7 0.3 [2,] 0.1 0.9 #create the Discrete Time Markov Chain MC 1 A 2 - dimensional discrete Markov Chain defined by the following states: Pepsi, Coke The transition matrix (by rows) is defined as follows: Pepsi Coke Pepsi 0.7 0.3 Coke 0.1 0.9
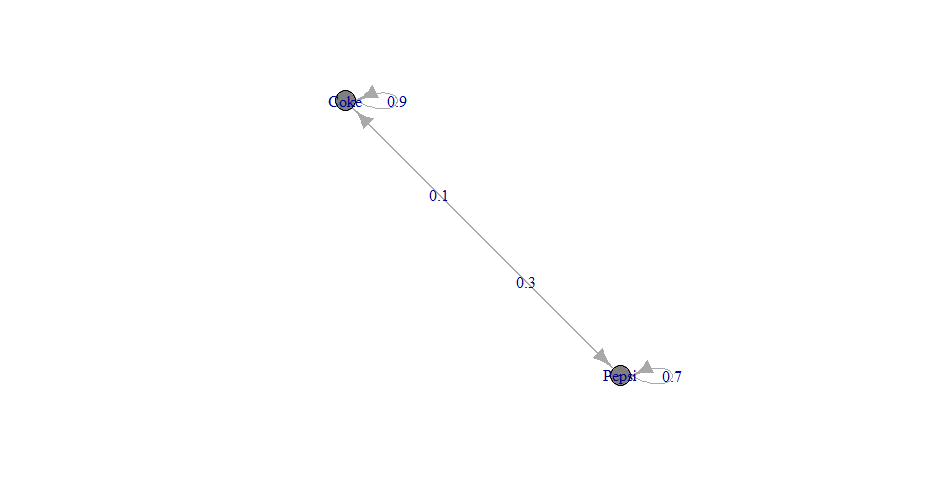
Trama
Paso 2: Calcular la participación de mercado después de 1 mes y 2 meses
Producción
#Market Share after one month Pepsi Coke 0.43 0.57 #Market Share after two month Pepsi Coke 0.358 0.642
Paso 3: creación de una matriz de estado estable
Producción
Pepsi Coke 0.25 0.75
Notas finales
En este artículo le presentamos las ecuaciones de cadena de Markov, la terminología y su implementación en R. También analizamos cómo se pueden escalar ecuaciones simples usando la multiplicación de matrices. Usaremos estas terminologías y marco para resolver un ejemplo de la vida real en el próximo artículo. También le presentaremos conceptos como nodo absorbente y cadena de Markov regular para resolver el ejemplo.
¿Le resultó útil el artículo? ¿Este artículo resolvió alguno de sus problemas existentes? ¿Has usado una cadena de Markov simple antes? Si lo hizo, comparta con nosotros sus pensamientos sobre el tema.
