Introducción
En el artículo anterior, Cómo dividir un árbol de decisión: la búsqueda para lograr nodos puros, comprendió los conceptos básicos de los árboles de decisión, como la división, la división ideal y los nodos puros. En este artículo, veremos uno de los algoritmos más populares para seleccionar la mejor división en árboles de decisión: Impureza de Gini.
Nota: Si está más interesado en aprender conceptos en un formato audiovisual, tenemos este artículo completo explicado en el video a continuación. Si no es así, puede seguir leyendo.
PD: si no ha leído el artículo anterior, es probable que tenga dificultades para comprender este artículo.
Entonces, hasta ahora hemos visto que el atributo «Clase» es capaz de estimar el comportamiento del estudiante, sobre jugar al cricket o no. Y este atributo está funcionando mucho mejor en comparación con las dos variables restantes, como «la altura» y «el rendimiento en la clase». Si recuerda, hicimos una división de todas las funciones disponibles y luego comparamos cada división para decidir cuál era la mejor. Así es como también funciona el algoritmo del árbol de decisiones.
Un árbol de decisión primero divide los nodos en todas las variables disponibles y luego selecciona la división que da como resultado los subnodos más homogéneos.
Homogéneo aquí significa tener un comportamiento similar con respecto al problema que tenemos. Si los nodos son completamente puros, cada nodoNodo es una plataforma digital que facilita la conexión entre profesionales y empresas en busca de talento. A través de un sistema intuitivo, permite a los usuarios crear perfiles, compartir experiencias y acceder a oportunidades laborales. Su enfoque en la colaboración y el networking hace de Nodo una herramienta valiosa para quienes desean expandir su red profesional y encontrar proyectos que se alineen con sus habilidades y objetivos.... solo contendrá una única clase y, por lo tanto, serán homogéneos. Así que intuitivamente puedes imaginar que Cuanto mayor sea la pureza de los nodos, mayor será la homogeneidad.
Impureza de Gini: un algoritmo de árbol de decisión para seleccionar la mejor división
Hay varios algoritmos que utiliza el árbol de decisiones para decidir la mejor división para el problema. Primero veamos el más común y popular de todos ellos, que es Impureza de Gini. Mide la impureza de los nodos y se calcula como:

Primero entendamos qué es Gini y luego le mostraré cómo puede calcular la impureza de Gini para la división y decidir la división correcta. Digamos que tenemos un nodo como este-
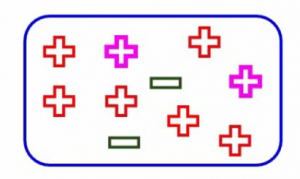
Entonces, lo que dice Gini es que si elegimos dos puntos de una población al azar, los rosados resaltados aquí, entonces deben ser de la misma clase. Digamos que tenemos un nodo completamente puro
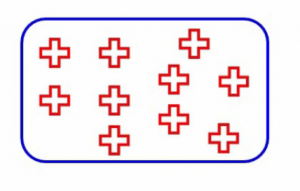
¿Puedes adivinar cuál sería la probabilidad de que un punto elegido al azar pertenezca a la misma clase? Bueno, obviamente será 1 ya que todos los puntos aquí pertenecen a la misma clase. Entonces, no importa qué dos puntos haya elegido, siempre pertenecerán a esa clase y, por lo tanto, la probabilidad siempre será 1 si el nodo es puro. Y eso es lo que queremos lograr con Gini.
Gini varía de cero a uno, ya que es una probabilidad y cuanto mayor sea este valor, mayor será la pureza de los nodos. Y, por supuesto, un valor menor significa nodos puros menores.
Propiedades de la impureza de Gini
Veamos sus propiedades antes de calcular la impureza de Gini para decidir la mejor división.
Decidimos la mejor división en función de la impureza de Gini y, como discutimos antes, la impureza de Gini es:

Aquí Gini denota la pureza y, por tanto, la impureza de Gini nos habla de la impureza de los nodos. Si se reduce la impureza de Gini, podemos inferir con seguridad que la pureza será mayor y, por lo tanto, una mayor probabilidad de homogeneidad de los nodos.
Gini funciona solo en aquellos escenarios en los que tenemos categórico objetivos. No funciona con objetivos continuos.
Un punto muy importante a tener en cuenta a tener en cuenta. Por ejemplo, si desea predecir el precio de la vivienda o la cantidad de bicicletas que se han alquilado, Gini no es el algoritmo adecuado. Solo realiza divisiones binarias, ya sea sí o no, éxito o fracaso, etc. Por lo tanto, solo dividirá un nodo en dos subnodos. Estas son las propiedades de la impureza de Gini.
Pasos para calcular la impureza de Gini para un Split
Veamos ahora los pasos para calcular la división de Gini. Primero, calculamos la impureza de Gini para los subnodos, como ya ha discutido, y estoy seguro de que ya lo sabe:
Impureza de Gini = 1 – Gini
Aquí está la suma de los cuadrados de las probabilidades de éxito de cada clase y se da como:
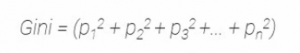
Considerando que hay n clases.
Una vez que hemos calculado la impureza de Gini para los subnodos, calculamos la impureza de Gini de la división utilizando la impureza ponderada de ambos subnodos de esa división. Aquí, el peso se decide por el número de observaciones de muestras en ambos nodos. Veamos estos cálculos usando un ejemplo, que lo ayudará a comprender esto aún mejor.
Para la división sobre el desempeño en la clase, ¿recuerdan que así fue la división?
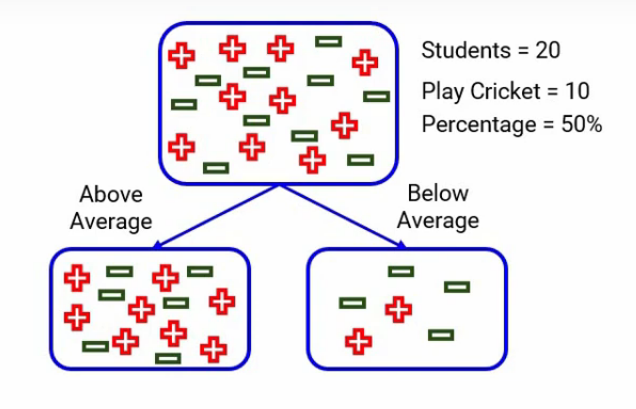
Dividir en rendimiento en clase
Tenemos dos categorías, una está «por encima del promedio» y la otra está «por debajo del promedio». Cuando nos enfocamos en el promedio anterior, tenemos 14 estudiantes de los cuales 8 juegan al cricket y 6 no. La probabilidad de jugar al cricket sería 8 dividido por 14, que es alrededor de 0,57, y de manera similar, para no jugar al cricket, la probabilidad será 6 dividida por 14, que será alrededor de 0,43. Aquí por simplicidad, he redondeado los cálculos en lugar de tomar el número exacto.
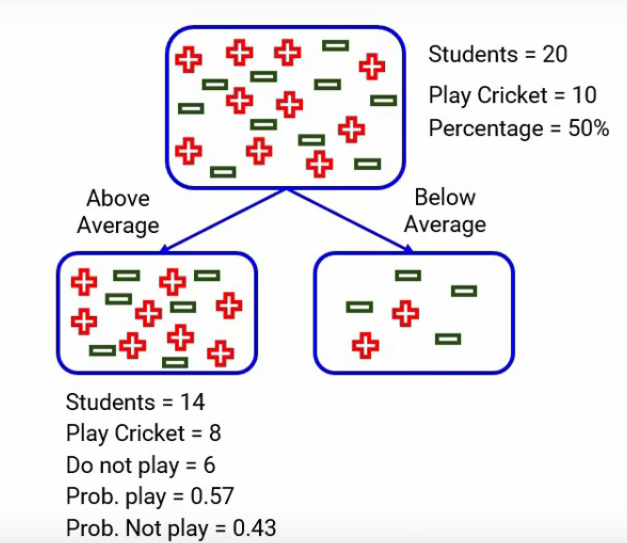
Del mismo modo, cuando miramos por debajo del promedio, calculamos todos los números y aquí están: la probabilidad de jugar es 0,33 y de no jugar es 0,67-
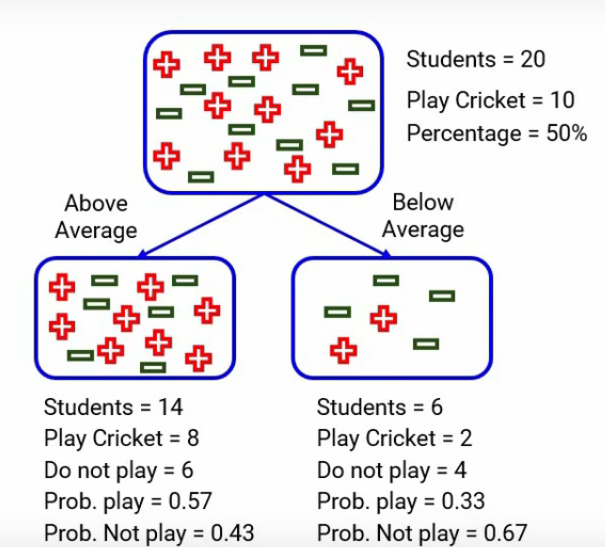
Calculemos ahora la impureza de Gini de los subnodos por encima del promedio y aquí está el cálculo:

Será, uno menos el cuadrado de la probabilidad de éxito para cada categoría, que es 0,57 para jugar al cricket y 0,43 para no jugar al cricket. Entonces, después de este cálculo, Gini sale a la luz 0,49. El nodo Inferior al promedio hará el mismo cálculo que Gini. Por debajo del promedio:

Viene alrededor de 0.44. Simplemente haga una pausa y analice estos números.
Ahora, para calcular la impureza de Gini de la división, tomaremos las impurezas de Gini ponderadas de ambos nodos, por encima del promedio y por debajo del promedio. En este caso, el peso de un nodo es el número de muestras en ese nodo dividido por el número total de muestras en el nodo padre. Entonces, para el nodo por encima del promedio aquí, el peso será 14/20, ya que hay 14 estudiantes que se desempeñaron por encima del promedio del total de 20 estudiantes que tuvimos.
Y el peso por debajo del promedio es 20/6. Entonces, la impureza de Gini ponderada será el peso de ese nodo multiplicado por la impureza de Gini de ese nodo. La impureza ponderada de Gini para rendimiento en clase dividida sale a ser:

De manera similar, aquí hemos capturado la impureza de Gini para la división de la clase, que sale a estar alrededor 0,32–

Ahora, si comparamos las dos impurezas de Gini para cada división-
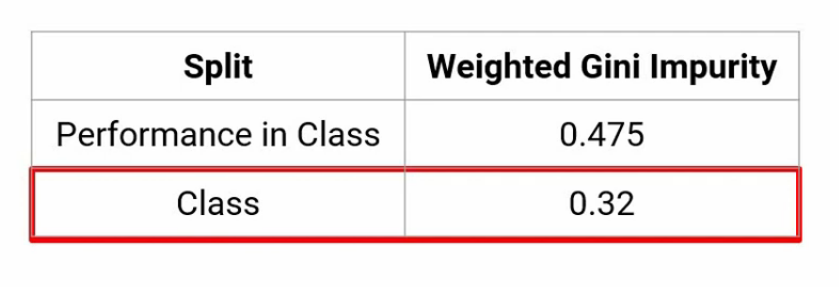
Vemos que la impureza de Gini para la división en Clase es menos. Y por lo tanto, la clase será la primera división de este árbol de decisiones.
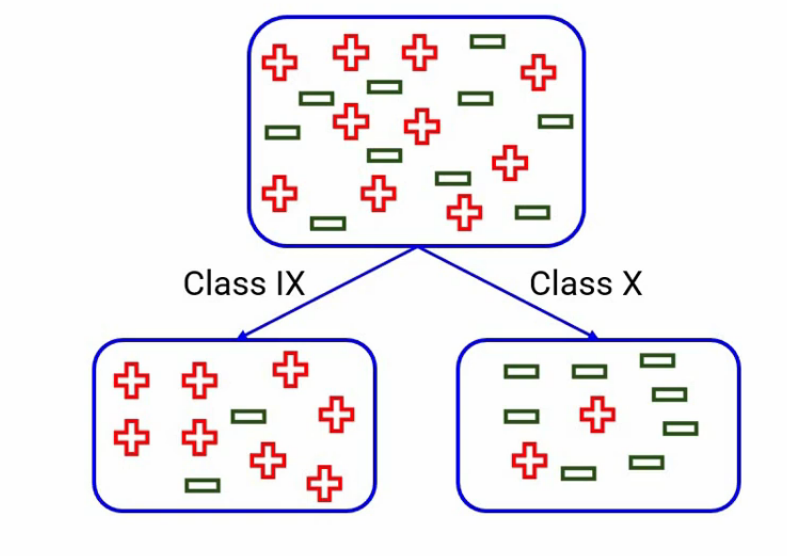
Dividir en clase
De manera similar, para cada división, calcularemos las impurezas de Gini y la división que produzca la impureza mínima de Gini se seleccionará como división. Y sabes, que el valor mínimo de impureza de Gini significa que el nodo será más puro y más homogéneo.
Notas finales
En este artículo, vimos uno de los algoritmos de división más populares en los árboles de decisión: la impureza de Gini. Solo se puede utilizar para variables de destino categóricas. Hay otros algoritmos que también se utilizan para dividir, que si quieres entender puedes hacérmelo saber en la sección de comentarios.
Si está buscando comenzar su viaje de ciencia de datos y desea todos los temas bajo un mismo techo, su búsqueda se detiene aquí. Eche un vistazo a la IA y ML BlackBelt certificadas de DataPeaker Más Programa
Si tienes alguna pregunta, ¡házmelo saber en la sección de comentarios!






