The tree begins with the nodeNodo is a digital platform that facilitates the connection between professionals and companies in search of talent. Through an intuitive system, allows users to create profiles, share experiences and access job opportunities. Its focus on collaboration and networking makes Nodo a valuable tool for those who want to expand their professional network and find projects that align with their skills and goals.... root that consists of the complete data and, subsequently, use smart strategies to divide nodes into multiple branches.
The original dataset was divided into subsets in this process.
To answer the fundamental question, your unconscious brain does some calculations (in light of the sample questions recorded below) and ends up buying the necessary amount of milk. Is it normal or during the week?
On working days we require 1 liter of milk.
It's a weekend? On weekends we need 1,5 liters of milk.
Is it correct to say that we are anticipating guests today? We need to buy 250 Additional ML of milk for each guest, and so on.
Before jumping to the hypothetical idea of decision trees, How about we initially explain what decision trees are? it's more, Why would it be a good idea for us to use them?
Why use decision trees?
Among other methods of supervised learningSupervised learning is a machine learning approach where a model is trained using a set of labeled data. Each input in the dataset is associated with a known output, allowing the model to learn to predict outcomes for new inputs. This method is widely used in applications such as image classification, speech recognition and trend prediction, highlighting its importance in..., tree-based algorithms excel. These are predictive models with greater precision and simple understanding.
How does the decision tree work?
There are different algorithms written to assemble a decision tree, which can be used for the problem.
Some of the most commonly used algorithms are listed below:
• TROLLEY
• ID3
• C4.5
• CHAID
Now we will explain about the CHAID algorithm step by step. Before that, we will talk a little about chi_square.
chi_square
Chi-Square is a measureThe "measure" it is a fundamental concept in various disciplines, which refers to the process of quantifying characteristics or magnitudes of objects, phenomena or situations. In mathematics, Used to determine lengths, Areas and volumes, while in social sciences it can refer to the evaluation of qualitative and quantitative variables. Measurement accuracy is crucial to obtain reliable and valid results in any research or practical application.... Statistics to find the difference between child and primary nodes. To calculate this, we found the difference between the observed and expected counts of the variableIn statistics and mathematics, a "variable" is a symbol that represents a value that can change or vary. There are different types of variables, and qualitative, that describe non-numerical characteristics, and quantitative, representing numerical quantities. Variables are fundamental in experiments and studies, since they allow the analysis of relationships and patterns between different elements, facilitating the understanding of complex phenomena.... target for each node and the sum squared of these standardized differences will give us the Chi-square value.
Formula
To find the most dominant feature, chi-square tests will use which is also called CHAID, while ID3 uses information gain, C4.5 uses the win ratio and CART uses the indexThe "Index" It is a fundamental tool in books and documents, which allows you to quickly locate the desired information. Generally, it is presented at the beginning of a work and organizes the contents in a hierarchical manner, including chapters and sections. Its correct preparation facilitates navigation and improves the understanding of the material, making it an essential resource for both students and professionals in various areas.... GINI.
Today, most programming libraries (for instance, Pandas for Python) use Pearson's metric for correlation by default.
The chi-square formula: –
√ ((Y – and ')2 / and ')
where y is real and is expected and '.
Data set
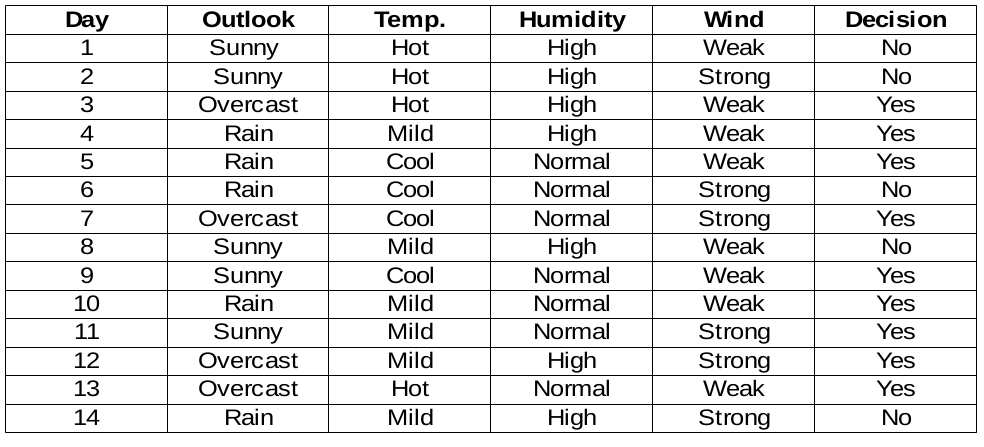
We are going to build decision rules for the following data set. The decision column is the target that we would like to find based on some characteristics.
By the way, we will ignore the day column because it is just the row number.
to read the Python implementation dataset from the CSV file below: –
import pandas as pd
data = pd.read_csv("dataset.csv")
data.head()
We need to find the most important characteristic in the target columns to choose the node to split the data in this dataset.
Moisture characteristic
There are two types of the class present in the humidity columns: tall and normal. Now we will calculate the chi_square values for them.
| Yes | No | Total | Expected | Chi-square Yes | Chi-square No | |
| High | 3 | 4 | 7 | 3,5 | 0,267 | 0,267 |
| low | 6 | 1 | 7 | 3,5 | 1.336 | 1.336 |
for each row, the total column is the sum of the yes and no decisions. Half of the total column is called expected values because there 2 classes in decision. It is easy to calculate the chi-square values based on this table..
For instance,
chi-square yes for high humidity is √ ((3– 3,5)2 / 3,5) = 0,267
while the real one is 3 and the expected is 3,5.
Then, the chi-square value of the humidity characteristic is
= 0,267 + 0,267 + 1,336 + 1,336
= 3.207
Now, we will also find chi-square values for other characteristics. The characteristic with the maximum chi-square value will be the decision point. What about the wind function?
Wind characteristic
There are two types of the class present in the wind columns: weak and strong. The following table is the following table.
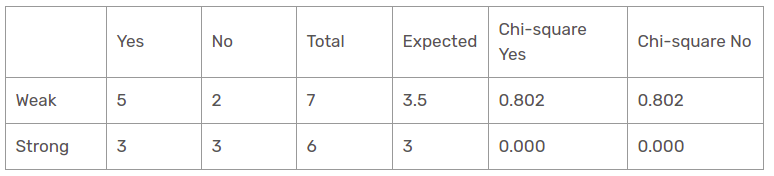
Here, the chi-square test value of the wind characteristic is
= 0,802 + 0,802 + 0 + 0
= 1,604
This is also a value less than the chi-square value of the humidity. What about the temperature function?
temperature characteristic
There are three kinds of the class present in the temperature columns: hot, cold and smooth. The following table is the following table.
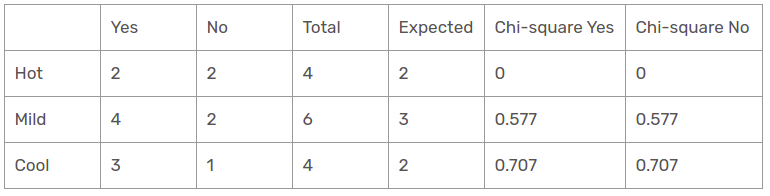
Here, the chi-square test value of the temperature characteristic is
= 0 + 0 + 0,577 + 0,577 + 0,707 + 0,707
= 2.569
This is a value less than the chi-square value of the humidity and also greater than the chi_square value of the wind. What about the Outlook function?
Outlook feature
There are three types of classes present in the temperature columns: sunny, rainy and cloudy. The following table is the following table.
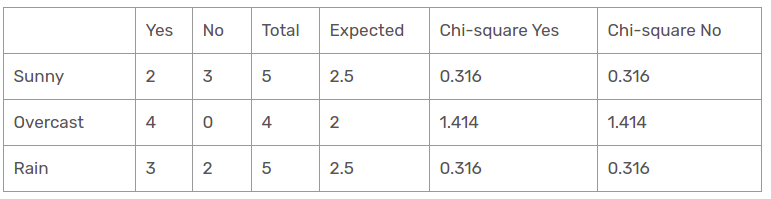
Here, the value of the chi-square test of the perspective function is
= 0,316 + 0,316 + 1,414 + 1,414 + 0,316 + 0,316
= 4.092
We have calculated the chi-square values of all the characteristics. Let's see them all at a table.
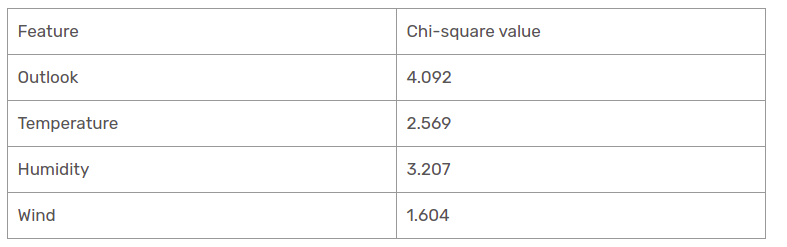
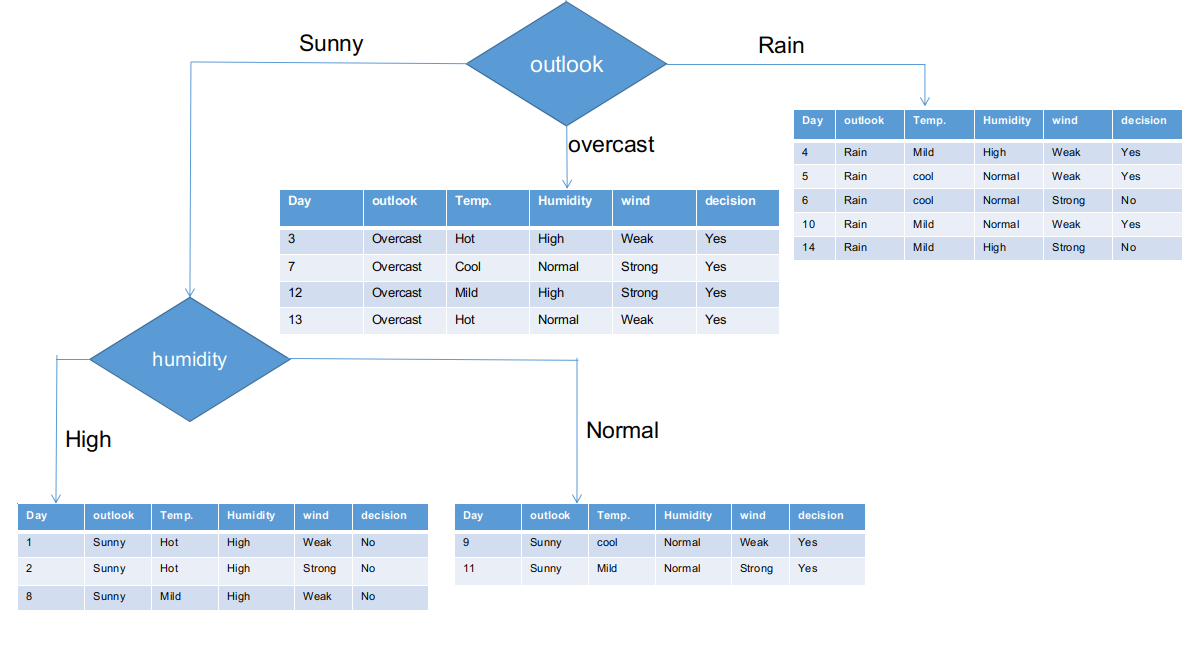
How it looks, the Outlook column has the highest and highest chi-square value. This implies that it is the main characteristic of the component. Along with these values, we will place this feature in the root node.
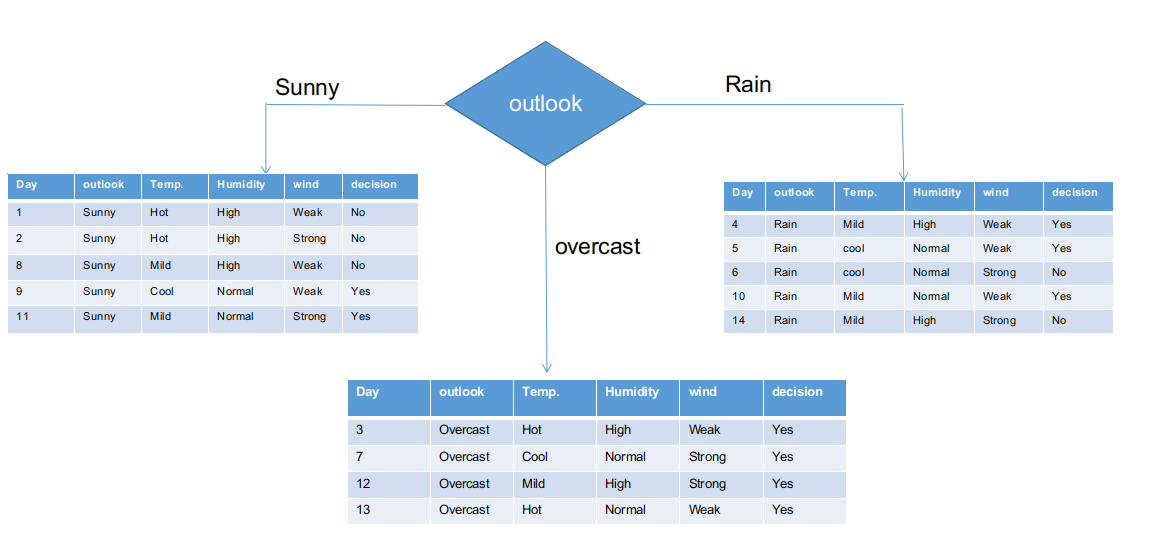
We have separated the raw information based on the Outlook classes in the above illustration. For instance, the clouded branch simply has an affirmative decision on the subinformation dataset. This implies that the CHAID tree returns YES if the panorama is cloudy.
Both sunny and rainy branches have yes and no decisions. We will apply chi-square tests for these subinformative data sets.
Outlook = sunny branch
This branch has 5 examples. Nowadays, we look for the most predominant characteristic. By the way, we will ignore the Outlook function now, since they are completely the same. At the end of the day, we will find the most predominant columns between temperature, humidity and wind.
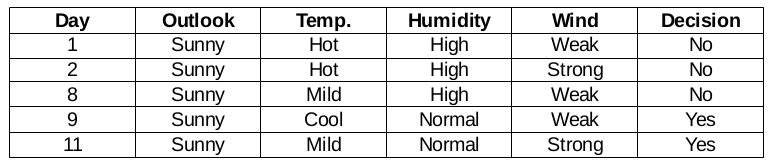
Humidity function for when the panorama is sunny
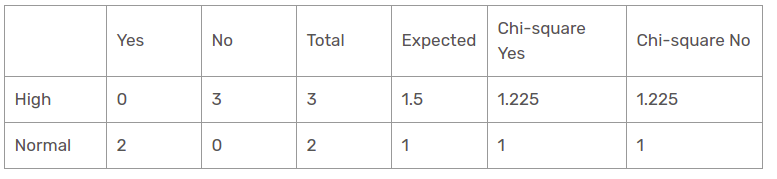
The chi-square value of the humidity characteristic for a sunny perspective is
= 1,225 + 1,225 + 1 + 1
= 4.449
Wind function for when the panorama is sunny
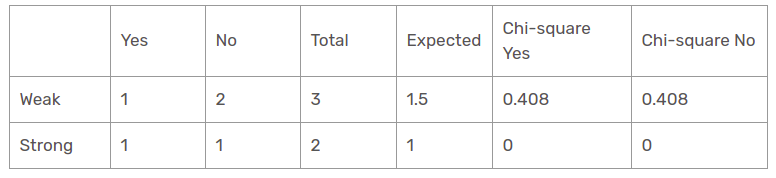
The chi-square value of the wind characteristic for sunny perspective is
= 0,408 + 0,408 + 0 + 0
= 0,816
Temperature function for when the panorama is sunny
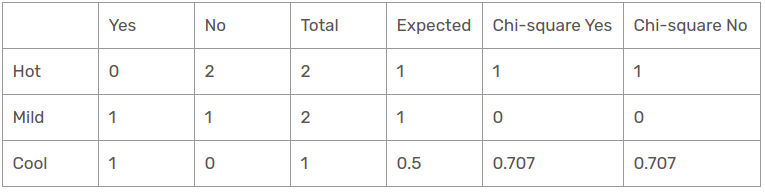
Then, the chi-square value of the temperature characteristic for sunny perspective is
= 1 + 1 + 0 + 0 + 0,707 + 0,707
= 3.414
We have found chi-square values for the sunny perspective. Let's see them all at a table.
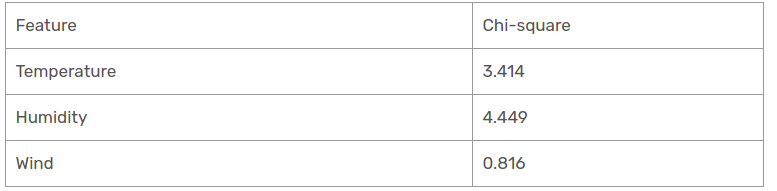
Nowadays, humidity is the most predominant feature of the sunny gazebo branch. We will put this characteristic as a decision rule.
Nowadays, both branches of humidity for sunny perspective have only one decision as outlined above. The CHAID tree will return NO for a sunny perspective and high humidity and will return YES for a sunny perspective and normal humidity.
Rain perspective branch
In reality, this branch has both positive and negative decisions. We need to apply the chi-square test for this branch to find an accurate decision. This branch has 5 different instances, as demonstrated in the attached subinformation collection dataset. How about we find out the most predominant characteristic between temperature, humidity and wind?
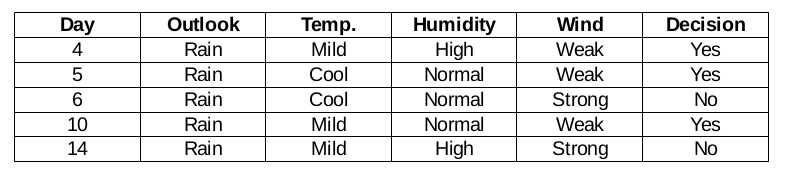
Wind function for rain forecast
There are two types of a class present in the wind characteristic for the rain perspective: weak and strong.
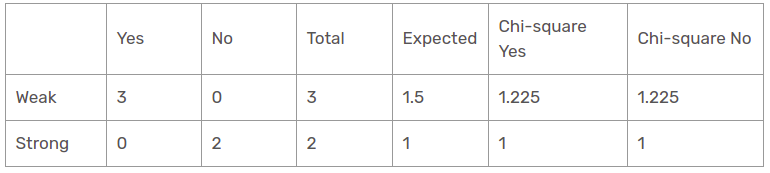
Then, the chi-square value of the wind characteristic for the rain perspective is
= 1,225 + 1,225 + 1 + 1
= 4.449
Humidity function for rain forecast
There are two kinds of a class present in the moisture characteristic for the rain perspective: tall and normal.
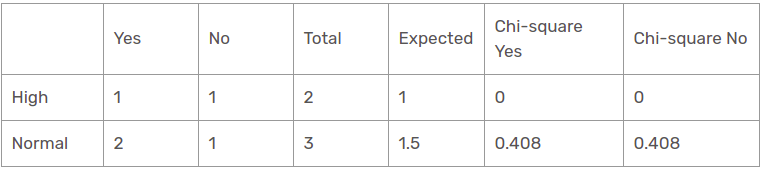
The chi-square value of the humidity characteristic for the rain perspective is
= 0 + 0 + 0.408 + 0.408
= 0,816
Temperature characteristic for rain forecast
There are two types of classes present in the temperature characteristics for the rain perspective, such as warm and cool.

The chi-square value of the temperature characteristic for the rain perspective is
= 0 + 0 + 0.408 + 0.408
= 0,816
We have found that all chi-square values for rain is the perspective branch. Let's see them all at one table.
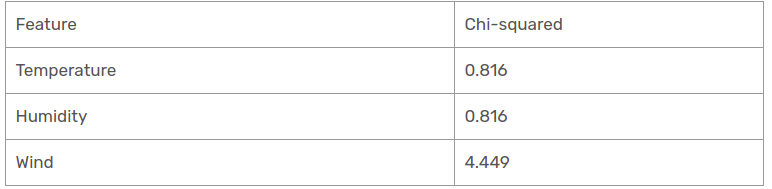
Therefore, the wind function is the winner of the rain is the perspective branch. Put this column in the connected branch and view the corresponding subinformative dataset.
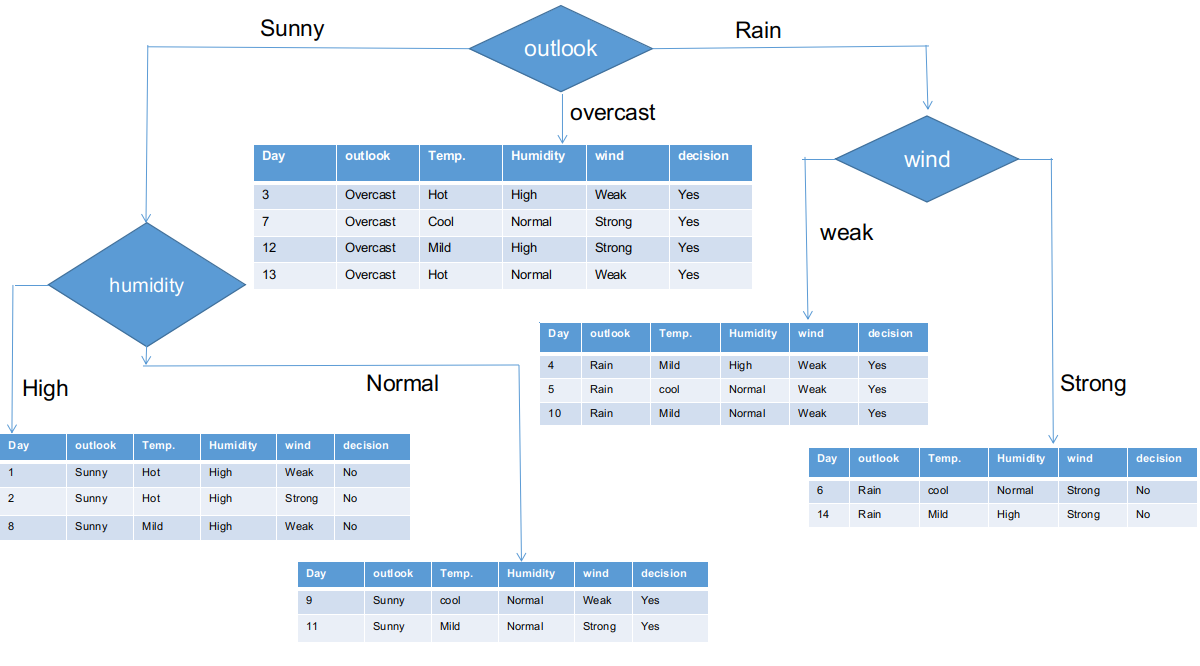
How it looks, all branches have subinformative data sets with a single decision, like yes or no. This way, we can generate the CHAID tree as illustrated below.
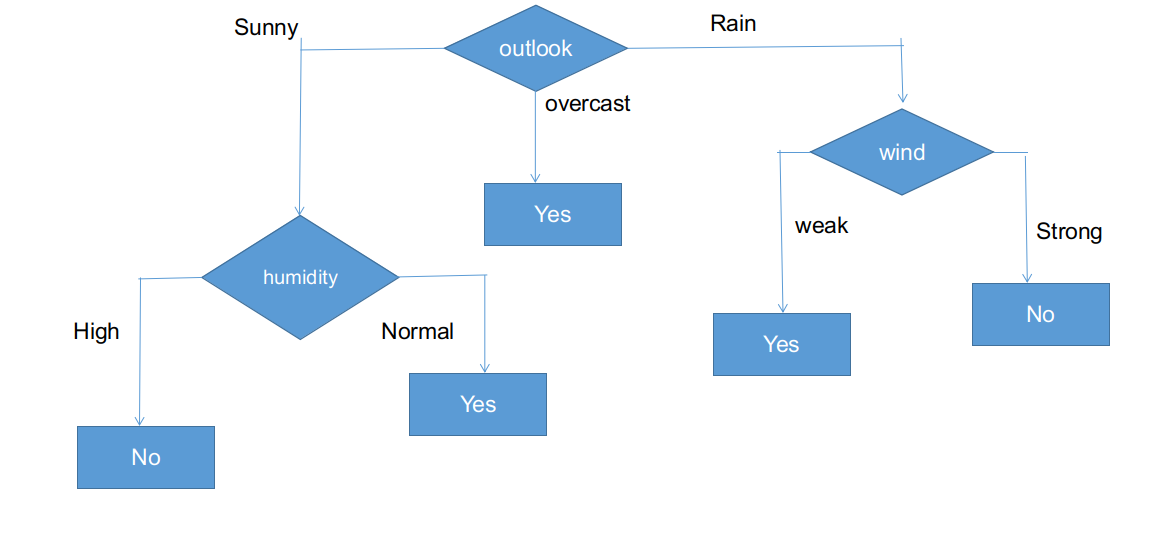
The final form of the CHAID tree.
Python implementation of a decision tree using CHAID
from chefboost import Chefboost as cb
import pandas as pd
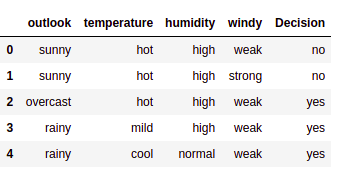
data = pd.read_csv("/home/kajal/Downloads/weather.csv")
data.head()
config = {"algorithm": "CHAID"}
tree = cb.fit(data, config)
tree
# test_instance = ['sunny','hot','high','weak','no'] test_instance = data.iloc[2] test_instance
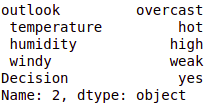
cb.predict(tree,test_instance)
output:- 'Yes'
#obj[0]: outlook, obj[1]: temperature, obj[2]: humidity, obj[3]: windy
# {"feature": "outlook", "instances": 14, "metric_value": 4.0933, "depth": 1}
def findDecision(obj):
if obj[0] == 'rainy':
# {"feature": " windy", "instances": 5, "metric_value": 4.4495, "depth": 2}
if obj[3] == 'weak':
return 'yes'
elif obj[3] == 'strong':
return 'no'
else:
return 'no'
elif obj[0] == 'sunny':
# {"feature": " humidity", "instances": 5, "metric_value": 4.4495, "depth": 2}
if obj[2] == 'high':
return 'no'
elif obj[2] == 'normal':
return 'yes'
else:
return 'yes'
elif obj[0] == 'overcast':
return 'yes'
else:
return 'yes'
Conclution
Therefore, we have created a CHAID decision tree from scratch to end on this post. CHAID uses a chi-square measurement metric to discover the most important characteristic and apply it recursively until sub-informative data sets have a single decision. Although it is a legacy decision tree algorithm, it's still the same process for sorting problems.
The media shown in this article is not the property of DataPeaker and is used at the author's discretion.






