This article was published as part of the Data Science Blogathon.
Overview
K-means clustering is a very famous and powerful unsupervised machine learning algorithm. Used to solve many complex unsupervised machine learning problems. Before starting, Let's take a look at the points that we are going to understand.
Table of Contents
- Introduction
- How does the K-means algorithm work?
- How to choose the value of K?
- Elbow method.
- Silhouette method.
- Advantages of k-means.
- Disadvantages of k-means.
Introduction
Entendamos el algoritmo de groupingThe "grouping" It is a concept that refers to the organization of elements or individuals into groups with common characteristics or objectives. This process is used in various disciplines, including psychology, Education and biology, to facilitate the analysis and understanding of behaviors or phenomena. In the educational field, for instance, Grouping can improve interaction and learning among students by encouraging work.. de K-means con su definición simple.
A K-means clustering algorithm attempts to cluster similar items as clusters. The number of groups is represented by K.
Let's take an example. Suppose you went to a vegetable store to buy some vegetables. There you will see different types of vegetables. The only thing you will notice there is that the vegetables will be arranged in a group of their types. As all carrots will stay in one place, potatoes will stick with their types and so on. If you notice here, then you will find that they are forming a group or group, where each of the vegetables is kept within its type of group forming the groups.
Ahora entenderemos esto con la ayuda de una hermosa figure"Figure" is a term that is used in various contexts, From art to anatomy. In the artistic field, refers to the representation of human or animal forms in sculptures and paintings. In anatomy, designates the shape and structure of the body. What's more, in mathematics, "figure" it is related to geometric shapes. Its versatility makes it a fundamental concept in multiple disciplines.....
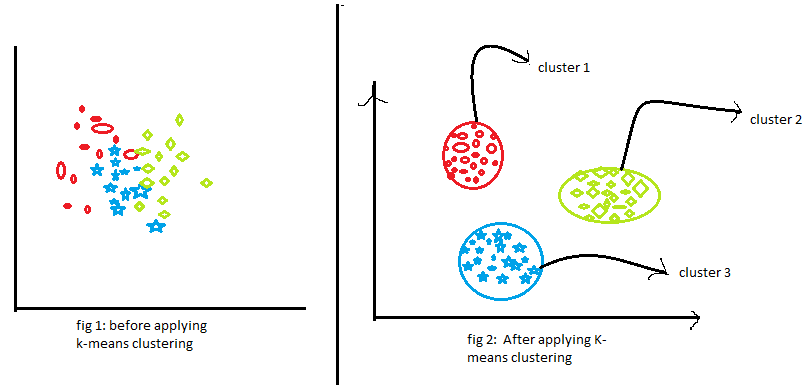
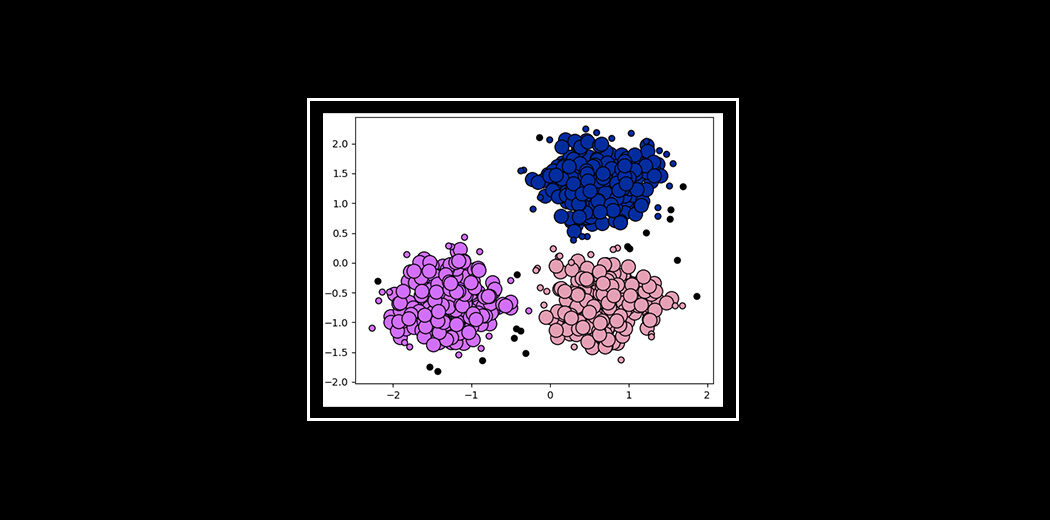
Now, look at the two figures above. What did you observe? Let's talk about the first figure. The first figure shows the data before applying the k-means clustering algorithm. Here the three different categories are messy. When you see that data in the real world, you will not be able to find out the different categories.
Now, look at the second figure (figure 2). This shows the data after applying the K-means clustering algorithm. you can see that the three different items are classified into three different categories which are called groups.
How does the K-means clustering algorithm work?
K-means grouping attempts to group similar types of items in the form of groupings. Find the similarity between the elements and group them into groups. The K-means clustering algorithm works in three steps. Let's see what these three steps are.
- Select the k values.
- Initialize the centroids.
- Select the group and find the average.
Let's understand the above steps with the help of the figure because a good image is better than thousands of words.
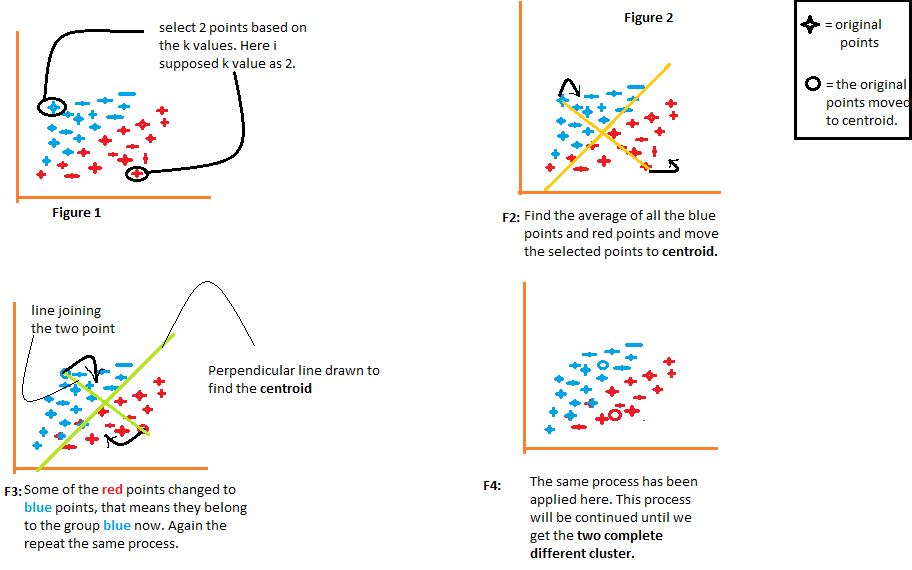
We will understand each figure one by one.
- The figure 1 shows the data representation of two different elements. the first element has been shown in blue and the second element has been shown in red. Here I choose the value of K randomly as 2. There are different methods by which we can choose the correct k values.
- In the figure 2, join the two selected points. Now, to find the centroid, we will draw a line perpendicular to that line. Points will move to their centroid. If you look there, you will see that some of the red dots now move to the blue dots. Now, these points belong to the group of blue elements.
- The same process will continue in the figure 3. We will join the two points and we will draw a line perpendicular to that and we will find the centroid. Now the two points will move to their centroid and again some of the red points will turn into blue points.
- The same process is happening in the figure 4. This process will continue until we get two completely different groups of these groups.
NOTE: Note that clustering K-means uses the Euclidean distance method to find out the distance between the points.
You will find many explanations about the Euclidean distance on the Internet.
How to choose the value of K?
One of the most challenging tasks of this clustering algorithm is choosing the correct values of k. What should be the correct k value? How to choose the k value? Let's find the answer to these questions. If you choose the k values at random, it may be right or wrong. If you choose the wrong value, will directly affect the performance of your model. Then, There are two methods by which you can select the correct value of k.
- Elbow method.
- Silhouette method.
Now, let's understand both concepts one by one in detail.
Elbow method
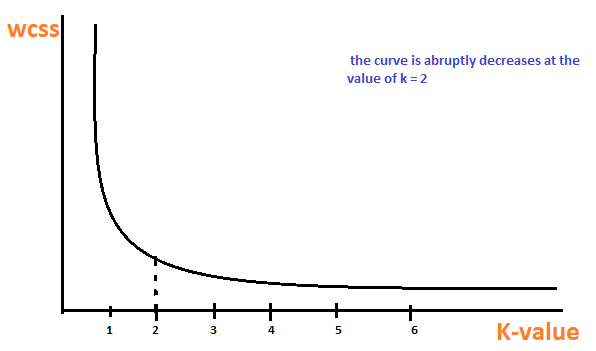
Elbow is one of the most famous methods by which you can select the correct value of k and increase the performance of your model. We also perform hyperparameter tuning to choose the best value of k. Let's see how this elbow method works.
It is an empirical method to find the best value of k. collect the range of values and take the best of them. Calculate the sum of the square of the points and calculate the mean distance.
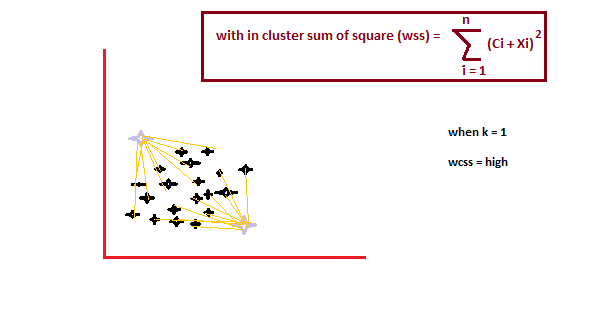
When the value of k is 1, the sum of the square within the group will be high. A measureThe "measure" it is a fundamental concept in various disciplines, which refers to the process of quantifying characteristics or magnitudes of objects, phenomena or situations. In mathematics, Used to determine lengths, Areas and volumes, while in social sciences it can refer to the evaluation of qualitative and quantitative variables. Measurement accuracy is crucial to obtain reliable and valid results in any research or practical application.... que aumenta el valor de k, the sum of the squared value within the group will decrease.
Finally, we will plot a graph between the k values and the sum of the square within the group to obtain the k value. We will examine the chart carefully. Sometime, our graph will decrease abruptly. That point will be considered as a value of k.
Silhouette method
The silhouette method is somewhat different. The elbow method also takes the range of k values and draws the silhouette graph. Calculate the silhouette coefficient of each point. Find the average distance of points within your group to (I) and the average distance of the points to their next closest group called b (I).

Note: The A (i) value must be less than b (I) value, what is ai << with a.
Now, we have the values of a (i) and b (i). we will calculate the silhouette coefficient using the following formula.
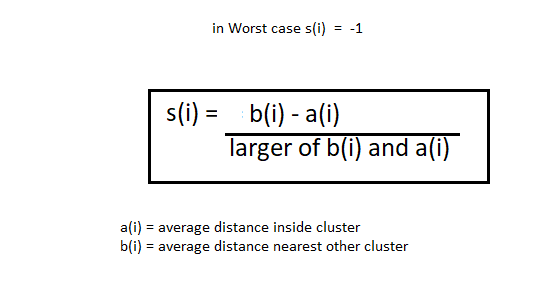
Now, we can calculate the silhouette coefficient of all the points in the groups and plot the silhouette graph. This graph will also be useful to detect outliers. The plot of the silhouette is between -1 a 1.
Note that for the silhouette coefficient equal to -1 is the worst case.
Look at the graph and verify which of the k values is closest to 1.
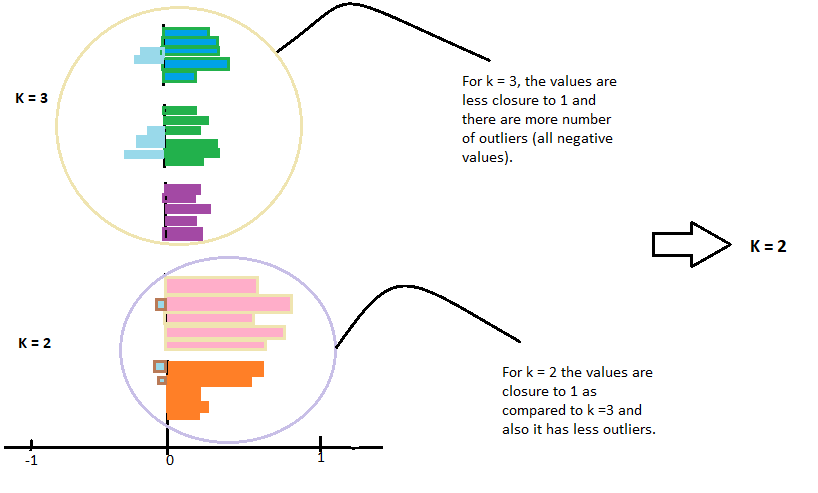
What's more, check the chart that has the least outliers, what a less negative value means. Then choose that value of k for your model to tune it.
Advantages of K-means
- It is very easy to implement.
- It is scalable to a large data set and also faster to large data sets.
- adapt new examples very often.
- Clusters generalization for different shapes and sizes.
Disadvantages of K-means
- It is sensitive to outliers.
- Choosing k-values manually is hard work.
- As the number of dimensions increases, its scalability decreases.