This article was published as part of the Data Science Blogathon
Introduction
In my previous article, I talk about the theoretical concepts about outliers and try to find the answer to the question: “When do we have to remove outliers and when do we keep outliers?”.
To better understand this article, you must first read that Article and then move on to this so that you have a clear idea about Outlier Analysis in Data Science Projects.
In this article, We will try to answer the following questions together with the Piton implementation,
👉 How to deal with outliers?
👉 How to detect outliers?
👉 What are the techniques for the detection and removal of outliers?
Let us begin
How to deal with outliers?
👉 Garrison: Exclude outliers. of our analysis. Applying this technique our data becomes thin when there are more outliers present in the data set. Its main advantage is its the fastest nature.
👉Tamponade: In this technique, Cap our outliers and make the limit namely, above or below a particular value, all values will be considered outliers, and the number of outliers in the data set gives that bounding number.
For instance, If you are working in the income function, people above a certain income level may behave in the same way as those with lower incomes. In this case, can limit the value of income to a level that keeps it intact and, Consequently, deal with outliers.
👉Treat outliers as a missing value: By assuming outliers as missing observations, treat them accordingly, namely, equal to missing values.
You can check the missing value item here
👉 Discretization: In this technique, when making the groups we include the outliers in a particular group and force them to behave in the same way as those of other points in that group. This technique is also known as Binning.
You can learn more about discretization here.
How to detect outliers?
👉 For normal distributions: Use empirical normal distribution relationships.
– The data points below media-3 * (sigma) or above media + 3 * (sigma) are outliers.
where mean and sigma are the average value Y Standard deviation of a particular column.
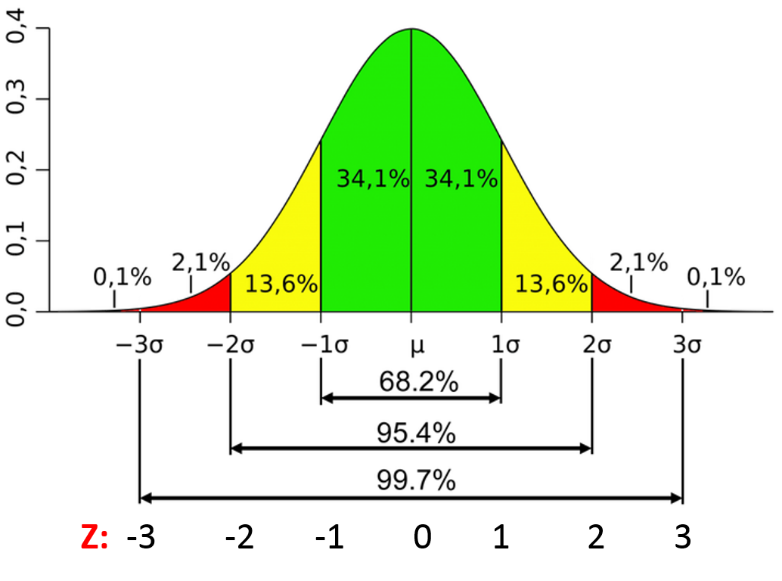
Fig. Characteristics of a normal distribution
Image source: Link
👉 For skewed distributions: Use the Inter-Quartile Range proximity rule (IQR).
– The data points below Q1 – 1.5 IQR or above Q3 + 1.5 IQR are outliers.
where Q1 and Q3 are the 25 Y Percentile 75 of the data set respectively, and IQR represents the interquartile range and is given by Q3 – Q1.

Fig. IQR to detect outliers
Image source: Link
👉 For other distributions: Use percentile-based approach.
For instance, Data points that are far from the percentile 99% and less than the percentile 1 are considered outliers.
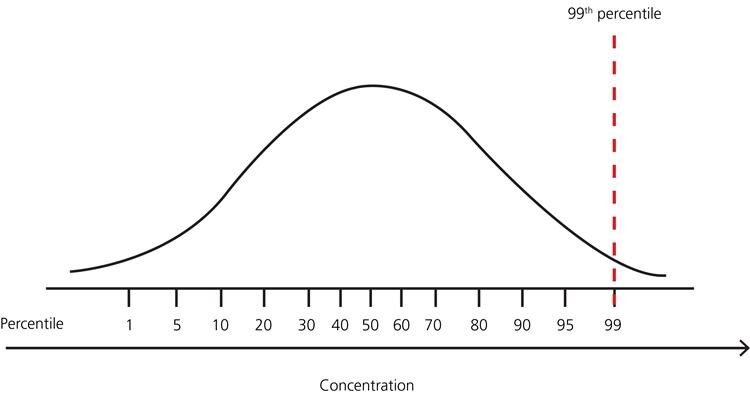
Fig. Percentile representation
Image source: Link
Techniques for the detection and elimination of outliers:
👉 Z score treatment:
Assumption– Characteristics are normally or approximately normally distributed.
Paso 1: Import of required dependencies
import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns
Paso 2: read and load the data set
df = pd.read_csv('placement.csv')
df.sample(5)Paso 3: Sketch the distribution graphs for the characteristics
import warnings
warnings.filterwarnings('ignore')
plt.figure(figsize=(16,5))
plt.subplot(1,2,1)
sns.distplot(df['cgpa'])
plt.subplot(1,2,2)
sns.distplot(df['placement_exam_marks'])
plt.show()Paso 4: find limit values
print("Highest allowed",df['cgpa'].mean() + 3*df['cgpa'].std())
print("Lowest allowed",df['cgpa'].mean() - 3*df['cgpa'].std())Production:
Highest allowed 8.808933625397177 Lowest allowed 5.113546374602842
Paso 5: find outliers
df[(df['cgpa'] > 8.80) | (df['cgpa'] < 5.11)]
Paso 6: Outlier trim
new_df = df[(df['cgpa'] < 8.80) & (df['cgpa'] > 5.11)] new_df
Paso 7: outlier limitation
upper_limit = df['cgpa'].mean() + 3*df['cgpa'].std() lower_limit = df['cgpa'].mean() - 3*df['cgpa'].std()
Paso 8: now, apply cap
df['cgpa'] = np.where(
df['cgpa']>upper_limit,
upper_limit,
np.where(
df['cgpa']<lower_limit,
lower_limit,
df['cgpa']
)
)Paso 9: now view the statistics using the function “Describe”
df['cgpa'].describe()
Production:
count 1000.000000 mean 6.961499 std 0.612688 min 5.113546 25% 6.550000 50% 6.960000 75% 7.370000 max 8.808934 Name: cgpa, dtype: float64
This completes our Z-score based technique!!
👉 Filtering based on IQR:
Used when our data distribution is skewed.
Paso 1: import the necessary dependencies
import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns
Paso 2: read and load the data set
df = pd.read_csv('placement.csv')
df.head()Paso 3: Sketch the distribution graph of the characteristics.
plt.figure(figsize=(16,5)) plt.subplot(1,2,1) sns.distplot(df['cgpa']) plt.subplot(1,2,2) sns.distplot(df['placement_exam_marks']) plt.show()
Paso 4: Form a box plot for the skewed characteristic
sns.boxplot(df['placement_exam_marks'])
Paso 5: Find the IQR
percentile25 = df['placement_exam_marks'].quantile(0.25) percentile75 = df['placement_exam_marks'].quantile(0.75)
Paso 6: Find the upper and lower limit
upper_limit = percentile75 + 1.5 * iqr lower_limit = percentile25 - 1.5 * iqr
Paso 7: find outliers
df[df['placement_exam_marks'] > upper_limit] df[df['placement_exam_marks'] < lower_limit]
Paso 8: Cutout
new_df = df[df['placement_exam_marks'] < upper_limit] new_df.shape
Paso 9: Compare the plots after clipping
plt.figure(figsize=(16,8)) plt.subplot(2,2,1) sns.distplot(df['placement_exam_marks']) plt.subplot(2,2,2) sns.boxplot(df['placement_exam_marks']) plt.subplot(2,2,3) sns.distplot(new_df['placement_exam_marks']) plt.subplot(2,2,4) sns.boxplot(new_df['placement_exam_marks']) plt.show()
Paso 10: plugged
new_df_cap = df.copy()
new_df_cap['placement_exam_marks'] = np.where(
new_df_cap['placement_exam_marks'] > upper_limit,
upper_limit,
np.where(
new_df_cap['placement_exam_marks'] < lower_limit,
lower_limit,
new_df_cap['placement_exam_marks']
)
)Paso 11: Compare the parcels after the limitation
plt.figure(figsize=(16,8)) plt.subplot(2,2,1) sns.distplot(df['placement_exam_marks']) plt.subplot(2,2,2) sns.boxplot(df['placement_exam_marks']) plt.subplot(2,2,3) sns.distplot(new_df_cap['placement_exam_marks']) plt.subplot(2,2,4) sns.boxplot(new_df_cap['placement_exam_marks']) plt.show()
This completes our IQR-based technique!!
👉 Percentile:
– This technique works by setting a particular threshold value, which decides based on our approach to the problem.
– While we remove outliers by limiting, that particular method is known as Winsorización.
– Here we always keep symmetry on both sides means that if we remove the 1% right, then on the left we also decrease a 1%.
Paso 1: import the necessary dependencies
import numpy as np import pandas as pd
Paso 2: read and load the data set
df = pd.read_csv('weight-height.csv')
df.sample(5)Paso 3: Sketch the distribution graph of the characteristic of “height”
sns.distplot(df['Height'])
Paso 4: Sketch the box plot of the characteristic of “height”
sns.boxplot(df['Height'])
Paso 5: Find the upper and lower limit
upper_limit = df['Height'].quantile(0.99) lower_limit = df['Height'].quantile(0.01)
Paso 7: apply trim
new_df = df[(df['Height'] <= 74.78) & (df['Height'] >= 58.13)]
Paso 8: Compare the distribution and the box plot after clipping
sns.distplot(new_df['Height']) sns.boxplot(new_df['Height'])
👉 Winsorización:
Paso 9: Apply limitation (Winsorización)
df['Height'] = np.where(df['Height'] >= upper_limit,
upper_limit,
np.where(df['Height'] <= lower_limit,
lower_limit,
df['Height']))Paso 10: Compare distribution and box plot after constraint
sns.distplot(df['Height']) sns.boxplot(df['Height'])
This completes our percentile-based technique!!
Final notes
Thank you for reading!
If you liked this and want to know more, visit my other articles on data science and machine learning by clicking on the Link
Feel free to contact me at Linkedin, Email.
Anything not mentioned or do you want to share your thoughts? Feel free to comment below and I'll get back to you.
About the Author
Chirag Goyal
Nowadays, I am pursuing my Bachelor of Technology (B.Tech) in Computer Science and Engineering from Indian Institute of Technology Jodhpur (IITJ). I am very excited about machine learning, the deep learningDeep learning, A subdiscipline of artificial intelligence, relies on artificial neural networks to analyze and process large volumes of data. This technique allows machines to learn patterns and perform complex tasks, such as speech recognition and computer vision. Its ability to continuously improve as more data is provided to it makes it a key tool in various industries, from health... y la inteligencia artificial.
The media shown in this article is not the property of DataPeaker and is used at the author's discretion.






